東大(04後1) r は正の実数として、角 θ は 0 < θ < π/2 を満たすとする。 xy 平面の原点 O を P0, (1,0) を P1 として点 P2, P3, ... を以下の条件 (a), (b), (c) が n = 0, 1, 2, ... に対して満たされるようにとる。 (a)　Pn+1Pn+2 = rPnPn+1 (b)　∠PnPn+1Pn+2 = θ (c)　Pn, Pn+2, Pn+3 は同一直線上にある。 このとき次の問に答えよ。 (1)　r を θ を用いて表せ。 (2)　点 Pn の座標を (xn,yn) とする。 　　複素数 zn = xn + yni を θ を用いて表せ。 (3)　数列 {xn}, {yn} がともに収束するための必要十分条件は 　　π/3 < θ < π/2 であることを証明せよ。 以下 π/3 < θ < π/2 とする。極限値 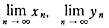をそれぞれ θ の関数と考えて α(θ), β(θ) とおく。 (4)　極限値 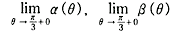をそれぞれ求めよ。 (5) π/3 < θ < π/2 における β(θ) の最大値を求めよ。 　　 　ヒント　　 　問題２　　 　問題３