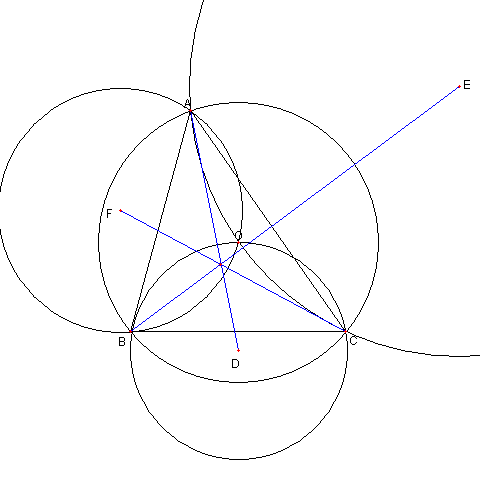
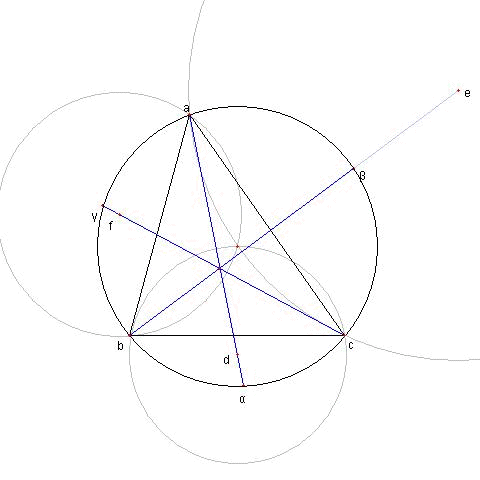
図において
O は鋭角三角形 ⊿ABC の外心とし
D, E, F は各々
⊿OBC, ⊿OCA, ⊿OAB の外心とする
このとき、
AD, BE, CF は一点で交わる
Gogeometryに紹介されていました
ここでは複素数をつかった証明を紹介します
⊿ABC の外接円が単位円となるよう
座標をいれて、複素数平面で考えよう
A, B, C, D, E, F に対応する複素数を
a, b, c, d, e, f とする
a, b, c は単位円上にある複素数である。
d が 0 と b を結ぶ垂直二等分線上にあるので
d + b2d = b
が成り立つ。(単位円と直線の方程式参照)
同様に
d + c2d = c
が成り立つ。
よって
d = 1/(b+c)
であり、 b, c の長さが 1 なので
d = bc/(b+c)
が成り立つ。
e = 1/(c+a), e = ca/(c+a)
f = 1/(a+b), f = ab/(a+b)
である
複素数を α とする。
d が長さが 1 の複素数 a と α を
結ぶ直線上にあるので
d + a αd = a + α
(単位円と直線の方程式参照)
よって
(ad - 1) α = a - d
d = 1/(b+c), d = bc/(b+c)
なので
α = (ca+ab-bc)/(a-b-c)
である。
複素数を β とし
c と f を結ぶ直線が単位円と再び交わる
複素数を γ とすると、同様にして
β = (ab+bc-ca)/(b-c-a)
γ = (bc+ca-ab)/(c-a-b)
が成り立つ。
δ = (α - b)(β - c)(γ- a)
+ (c - α)(a - β)(b - γ)
とおくとき、
a と α, b と β、 c と γ を各々結ぶ3本の直線が
一点で交わることを示すには
δ = 0
を示せばよい。 (円のチェバ型定理参照)
α = (ca+ab-bc)/(a-b-c)
β = (ab+bc-ca)/(b-c-a)
γ = (bc+ca-ab)/(c-a-b) より
α - b = (b2 + ca)/(a-b-c), c - α = -(c2 + ab)/(a-b-c)
β - c = (c2 + ab)/(b-c-a), a - β = -(a2 + bc)/(b-c-a)
γ - a = (a2 + bc)/(c-a-b), b - γ = -(b2 + ca)/(b-c-a)
なので δ = 0 である
複素数平面における直線の方程式は
かなり複雑な式になる。 しかし、単位円に関連すると 簡単になり取り扱い安いものになる。
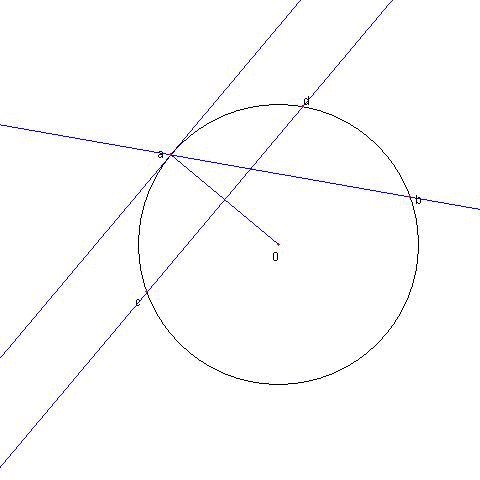
定理
a, b を長さ 1 の複素数とするとき
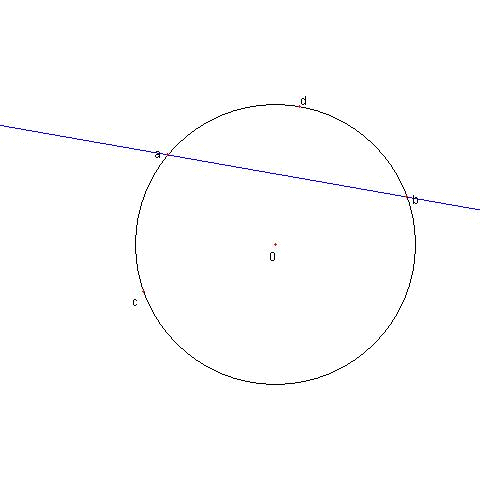
① a, b を通る直線の方程式は
z + abz = a + b
② a における単位円の接線の方程式は
z + a2z = 2a
③ 0 と a を結ぶ直線の垂直二等分線の
方程式は
z + a2z = a
必要十分条件は
(z-a)/(b-a) が実数である
つまり共役をとっても不変、従って
(z-a)( b - a) = (z - a)(b-a)
a, b は長さが 1 なので
a = 1/a, b = 1/b であるので
上記の式は
(z-a)(a - b)/ab = = (z - 1/a)(b-a)
これに ab/(a-b) をかけて
z-a = -ab(z - 1/a)
つまり
z + abz = a + b
を得る。(① が示せた)
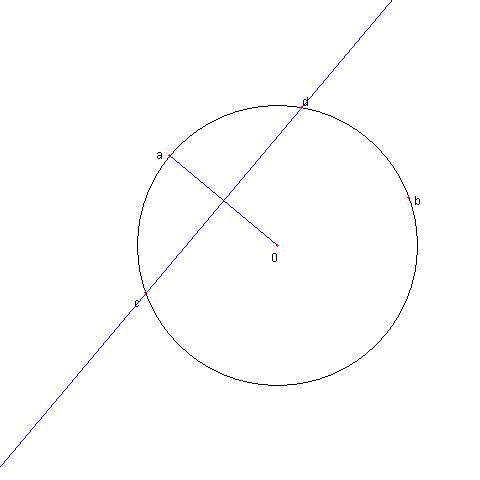
単位円との交点をに対応する複素数を
c, d とおくと
cd = a2 で c+d = a なので
① より垂直二等分線の方程式は
z + a2z = a
即ち ③ を得た。
(z-a)/a が純虚数、共役をとると符号が変わる
これを計算して②をえる。
(結果的に、①において b=a としたものですが
)
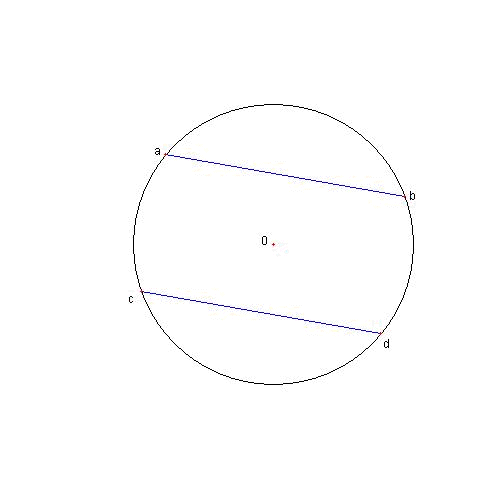
a と b を結ぶ直線と
c と d を結ぶ直線について
④ 平行である条件は ab = cd である。
⑤ 直交する条件は ab + cd = 0 である。
証明
④ 平行である条件は (c-d)/(a-b) が実数であること
つまり
(c-d)(a-b) = (a-b)(c-d) となる
a = 1/a, b = 1/b, c = 1/c, d = 1/d より
それは ad = cd となる
⑤ 直交する条件は (c-d)/(a-b) が純虚数であること
(c-d)(a-b) = -(a-b)(c-d) となる
a = 1/a, b = 1/b, c = 1/c, d = 1/d より
それは ad + cd = 0 となる
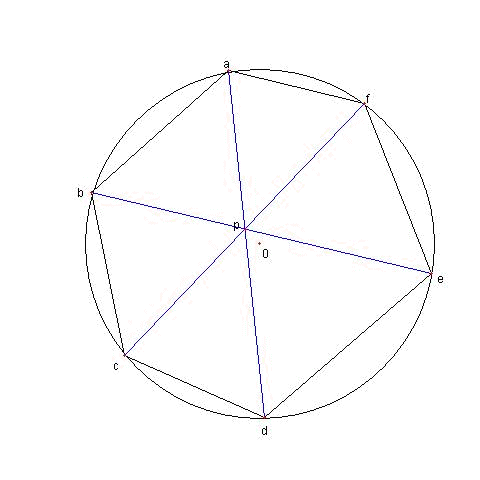
a, b, c, d, e, f を
複素数平面における単位円上の複素数とする
a と d, b と e, c と f を結ぶ
三本の直線が
一点で交わるまたは、 平行である
為の必要十分条件は
φ = (a-b)(c-d)(e-f)+(f-a)(b-c)(d-e)
とおくとき φ = 0 である
次を使う
補題
φ = ad(c+f-b-e) + (a+d)(be-cf)
- be(c+f) + cf(b+e)
補題の証明
φ を変形しよう
φ = a(c-d)(e-f) - b(c-d)(e-f)
+ f(b-c)(d-e) - a(b-c)(d-e)
= ac(e-f) -ad(e-f) - bc(e-f) + db(e-f)
+ df(b-c) - fe(b-c) - ad(b-c) + ae(b-c)
= ad(c-b+f-e)
+ a(ce-cf+be-ce) + d(be-bf+be-cf)
- bce + bcf -feb + fce
= ad(c+f-b-e) + (a+d)(be-cf)
- be(c+f) + cf(b+e)
補題が証明された

三本の直線が
複素数 p で交わっているとする
単位円の幾何学 より
p + adp = a+d
p + bep = b+e
p + cfp = c+f
が成り立つので
φ = ad(c+f-b-e) + (a+d)(be-cf)
- be(c+f) + cf(b+e)
= ad(p + cfp - p - bep )
+ (p + adp) (be-cf)
- be(p + cfp) + cf(p + bep)
= 0
が成り立つ。
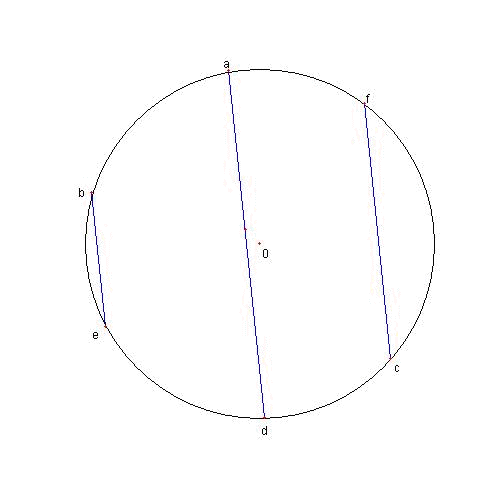
ad = be = cf
なので
φ = ad(c+f-b-e) + (a+d)(be-cf)
- be(c+f) + cf(b+e)
= ad(c+f-b-e) + (a+d)(ad-ad)
- ad(c+f) + ad(b+e)
= 0
が成り立つ。
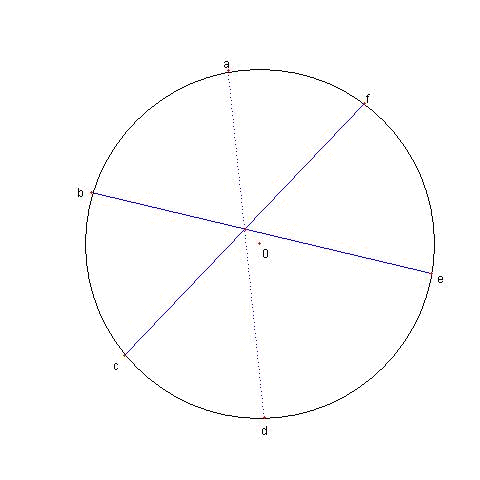
b と e を結ぶ直線と c と f を結ぶ直線が
平行でなく
複素数 p で交わっているとする
このとき be - cf ≠ 0 であり
p + adp = a+d
p + bep = b+e
である。
φ = ad(c+f-b-e) + (a+d)(be-cf)
- be(c+f) + cf(b+e)
= ad(p + cfp - p - bep )
+ (a+d) (be-cf)
- be(p + cfp) + cf(p + bep)
= (be-cf)(adp - a - d + p)
である。
φ = 0 かつ be - cf ≠ 0 なので
p + adp = a+d
をえる。これは p が a と d を結ぶ直線上に
あることを示している
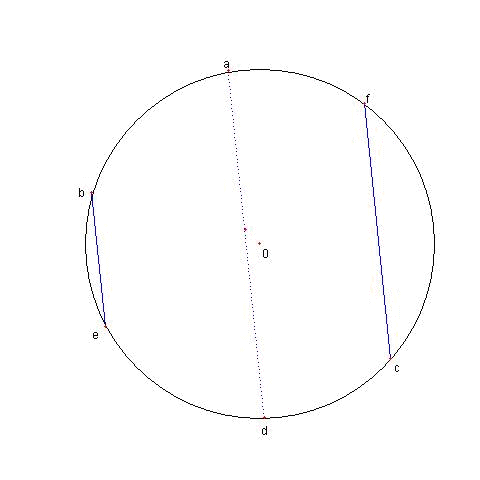
φ = ad(c+f-b-e) + (a+d)(be-cf)
- be(c+f) + cf(b+e)
= (ad - be)(c+f-b-e)
φ = 0 より
ad - be = 0 または c+f-b-e = 0
ad = be のときは
a と d を結ぶ直線と b と e を結ぶ直線は
平行である
c+f = b+e のときは
b と e を結ぶ直線と
c と f を結ぶ直線は一致する
(平行で共通点を持つので)