解答 (1)　z が 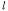上の点とするこのとき z = iz が 成り立っている。 α = iβ のときは |z-α| = |i(z-β)| = |z-β| である。 α = β のときは z-β は z-α と共役なので二つは長さおなじ これらより (1) が成り立つ。 (2)　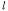 の全ての点 z に対して |(z-β)/(z-α)| = 1 つまり |z-β| = |z-α| とする。 0 は 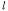の点なので z = 0 の時も上の式は成り立つので |β| = |α| つまり ββ = αα である。 z = 1+i とおくと z は 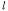の点であり z = iz で z ≠ 0 である。 |z-β|2 = (z-β) (z-β) = zz - z β - zβ + ββ |z-α|2 = (z-α) (z- α) = zz - zα - zα + αα であり |z-β|2 = |z-α|2、 ββ = αα、 z = iz 、 z ≠ 0　より β + iβ = iα + α が成り立つ。 β + iβ = iα + α で β (iβ) = (iα) α であるから α = β または α = iβ である。 (a = β + iβ = iα + α , b = β (iβ) = (iα) α とおくと β, iβ は x2 - ax + b = 0 の解で、 iα、 α も x2 - ax + b = 0 の解であるから) (もう少し精密な解釈は後で示す) (3)　z1, z2, γ は題意のものとする。 z1 = iz1, z2 = iz2, で z1 ≠ z2 である。 z1 - β = γ(z-α) = γ(iz1-α) で z2 - β = γ(z-α) = γ(iz2-α) であるから z1 - z2 = iγ( z1 - z2) を得て z1 - z2 ≠ 0 であるから 1 = iγ つまり γ = -i である。 z1 - β = γ(z-α) = γ(iz1-α) = z1 + iα より β = -iα である z を 上の任意の点とすると、 z = -iz である。 z - β = -iz + iα = -i(z-α) = γ(z-α) である。 これより (3) が示された。もちろん γ = -i である。 戻る 　 (2) の精密な解釈 β + iβ = iα + α で β (iβ) = (iα) α であるから (α-β) (α-iβ) = α2 - (β+iβ)α + β(iβ) 　= α2 - (iα + α)α + (iα) α = (α-iα)(α-α) = 0 であるから α = β または α = iβ である。