とおくこのとき
∫1n+1 x/(n2+x2)dx < In < ∫0nx/(n2+x2)dx
であり
∫1n+1 x/(n2+x2)dx = (1/2) (log(n2+(n+1)2) - log(n2+12)
∫0n x/(n2+x2)dx = (1/2) (log(n2+n2) - log(n2) = (1/2) log2
などより
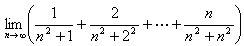 = (1/2) log2 を得る
= (1/2) log2 を得る
戻る
indexに戻る
|
(3) In = 1/(n2+12) + 2/(n2+22)
+ 3/(n2+32) + ... + n/(n2+n2) とおくこのとき ∫1n+1 x/(n2+x2)dx < In < ∫0nx/(n2+x2)dx であり ∫1n+1 x/(n2+x2)dx = (1/2) (log(n2+(n+1)2) - log(n2+12) ∫0n x/(n2+x2)dx = (1/2) (log(n2+n2) - log(n2) = (1/2) log2 などより 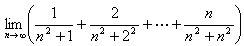 = (1/2) log2 を得る = (1/2) log2 を得る
戻る indexに戻る |