AB = BC = CA = 2 であった。
A から BC に引いた垂線の足を D とし
B から CA に引いた垂線の足を E とする。
D は BC の中点で E は CA の中点である。
図の対称性より AD は H をとおり
AD =
で
BE =
である。(増加を押す)BH = BE =
なので
HD = 
を得る。よって AH =
-
である。(増加を押す)H 及び I より下ろした垂線の足を
各々 J と K とおすと
BK = AJ = AH×(
/2) で
HI = JK = AB-AJ-KB なのでHI =
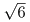- 1 である。(増加を押す)以下は付録
BE は HG を垂直ニ等分するので
θ = ∠HBE とおくと
sin θ = (HG/2)/BH = HI/(2
)
= /2 - /6 である。よって θ = sin-1(
/2 - /6) である。
(増加を押す)この θ を使えば扇形 GBH の面積が求められる。(増加を押す)
BE と HG との交点を L とおけば
BL = BE-LE = BE-AH/2 = (
+)/2 で
HG = HI = 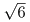- 1 でありBL と HG が直交しているので
僣BG の面積が求められる。
よって、残った空色の部分の面積がわかる。(増加を押す)
黄色の部分の面積も容易にわかる。