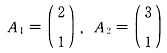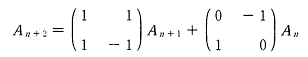、
、(n = 1, 2, 3, ...)|
解答 Anの第一成分を an, 第二成分を bn とおく。このとき a1 = 2, a2 = 3 b1 = 1, b2 = 1 an+2 = an+1 + bn+1 - bn ..... @ bn+2 = an+1 - bn+1 + an ..... A を得る。 cn = an+1 - bn dn = bn+1 - an (n = 1, 2, 3, ...) とおく @ より cn+1 = an+2 - bn+1 = an+1 - bn = cn よって cn = c1 = 2 (n = 1, 2, 3, ...) A より dn+1 = bn+2 - an+1 = - bn+1 + an = - cn よって dn = (-1)n-1c1 = (-1)n (n = 1, 2, 3, ...) |
an+2 = cn+1 + bn+1 =
2 + dn + an an+2 = 2 + (-1)n + an よって m を自然数とするとき a2m = 3(m-1) + a2 = 3m a2m-1 = m - 1 + a1 = m + 1 m を 2 以上の自然数とするとき b2m = d2m-1 + a2m-1 = m b2m-1 = d2m-2 + a2m-2 = m = 1 + 3(m-1) b2m = m, b2m-1 = 3m-2 これは m = 1 の時も成り立つ。 (後は答えを書くだけ) |