|
|
|
|
|
|
|
|
|
|
|
|
|
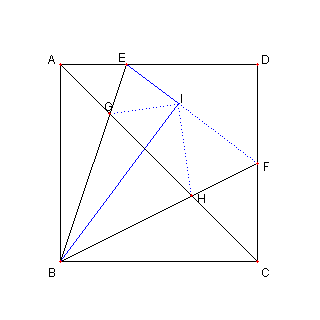
正方形と対角線と 45°
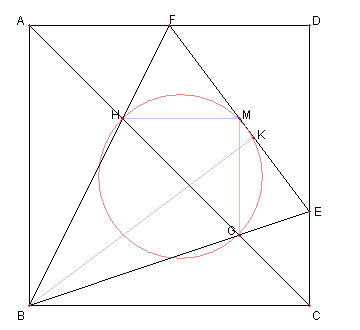
図において
四辺形 ABCD は正方形
E は CD 上の点で、 F は DA 上の点で
∠EBF = 45°とする
このとき、次を示せ。
① F, H, G, E, D は EF を直径とする
円の円周上にある。
② EF2 = 2 GH2
③ GH2 = AH2 + CG2
解説
Applet 版
|
|
|
派生問題
K を B から EF に下ろした垂線の足
M を EK の中点とすると
次が成り立つ。
④ H, G, K, M は同一円周上にある
⑤ GM ∥ CD, HM ∥ AD
|
|
|
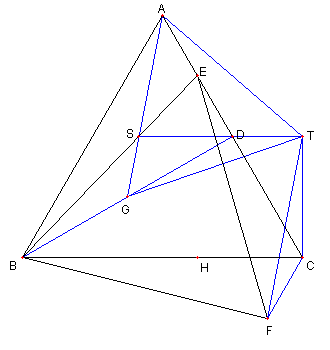
三つの正三角形
図において
⊿ABC を正三角形とする。
D は AC の中点、 E は AD の中点とする。
G は BD の中点とする。
⊿BFE, ⊿AGT は正三角形とする。
S は BE と AG との交点とする。
この時次を示せ
① S, D, T は BC と平行な一直線上にある。
② ⊿DGT ≡ ⊿CTF である。
③ ⊿GTF は正三角形である。
解説は抜きです
|
|
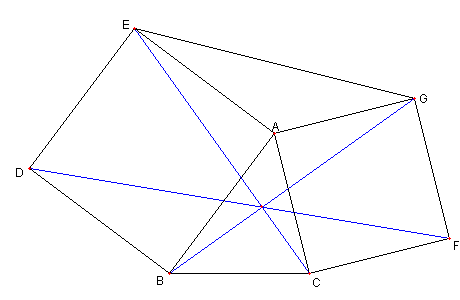
二つの正方形と二つの直角二等辺三角形
図において
四辺形 ABDE と ACFG は正方形とする。
このとき
EC, DF, BG が一点で交わることを示せ
解説
Applet 版
|
|
|
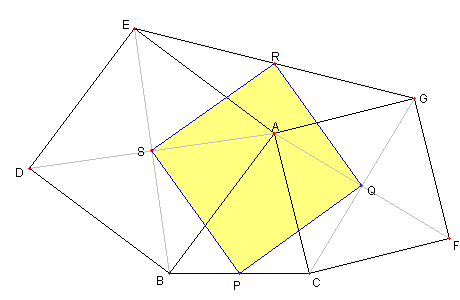
二つの正方形と二つの直角二等辺三角形
図において
四辺形 ABDE と ACFG は正方形とする。
P は BC の中点、R は EG の中点としし
Q は正方形 ACFG の中心、
S は正方形 ABDE の中心とする
このとき
四辺形 PQRS が正方形であることを示せ
解説
Applet 版
|
|
|
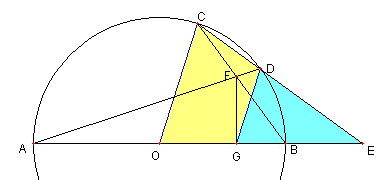
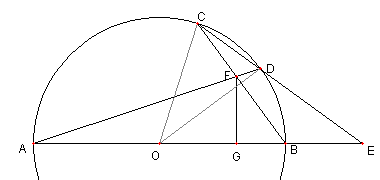
36°72°問題
図において
C, D は O を中心とし
直径 AB の円周上の点で
∠BOD = 36°, ∠BOC = 72°とする。
E は直線 CD と AB との交点、
F は直線 AD と BC との交点、
G は F から AB に下ろした垂線の足とする。
このとき、次を示せ
EG = OB, CD = OG
解説
Applet 版
|
|
|
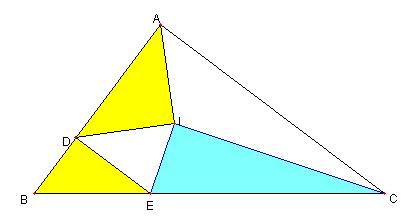
4つの直角三角形
⊿ABC を ∠BAC = 90°の直角三角形
I を ⊿ABC の内心とする。
D は AB 上の点で ∠AID = 90°
E は BC 上の点で ∠BDE = 90°とする。
このとき
∠EIC = 90°であることを示せ。
解説
Applet 版
|
|
|
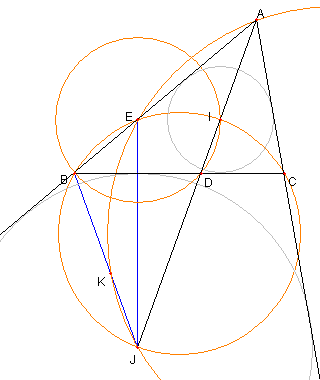
60°,40°,80°の三角形と内心と傍心
⊿ABC は ∠BAC = 60°, ∠ABC = 40°, ∠ACB = 80°
の三角形で I はその内心
J は ∠BAC 内にある傍接円の中心(傍心)
E は J を通り BC に垂直な直線と AB との交点
K は BK = AI なる BJ 上の点とする
このとき、次を示せ。
① I, D, B は E を中心とした円の円周上にある
② B, J, C, I, E は同一円周上にある
③ A, E, K, J は同一円周上にある
解説
Applet 版
|
|
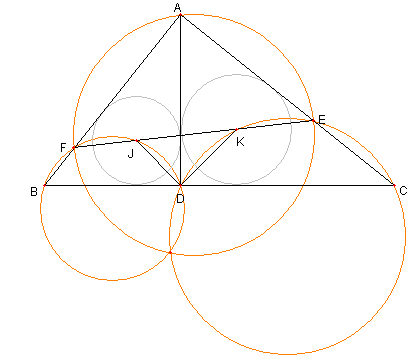
直角三角形と垂線と内心と外接円
⊿ABC は ∠°の直角三角形
D は A から BC に下ろした垂線の足
J, K は各々 ⊿ABD, ⊿ACD の内心
E , F は JK と各々 AC, AB との交点
とする。このとき次を示せ
① 四辺形 DCEK は円に内接する
② 四辺形 BDJF は円に内接する
③ 四辺形 DCEK の外接円
四辺形 BDJF の外接円
⊿AFE の外接円は一点で交わる
ヒント図
Applet 版
|
|
|
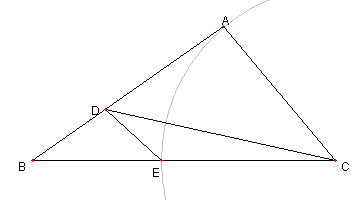
角度の問題
図において
D, E は各々辺 AB, BC 上の点で
∠DCB = α, ∠ACD = 3α, ∠BAC = 120°- 2α
CE = CA とする。このとき
∠CDE を求めよ。
ヒント図
Applet 版
|
|
|
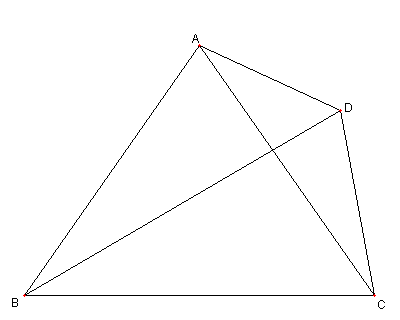
角度の問題
図において
AB = AC
∠ADB = 55°、∠BDC = 70°
とする。このとき
∠BAC を求めよ。
ヒント図
Applet 版
|
|
|
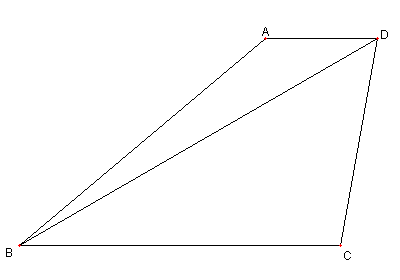
角度の問題
図において
AD と BC は平行
∠ABD = 10°、∠DBC = 30°
BA = BC
とする。このとき
∠BDC を求めよ。
ヒント図
Applet 版
|
|
|
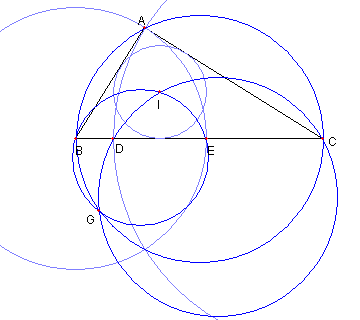
直角三角形と内心3
⊿ABC は ∠BAC = 90°の直角三角形として
I はその内心とする
D は BC 上の点で CD = CA とすし
E は BC 上の点で BE = BA とする
このとき、次を示せ
⊿ABC, ⊿IBE, ⊿IEC の
各々の外接円は一点で交わる
ヒント図
Applet 版
|
|
|
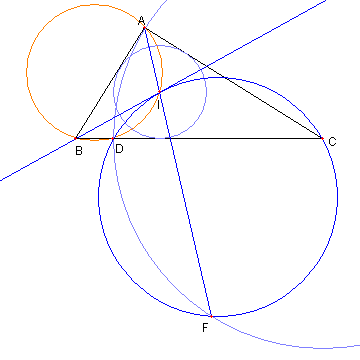
直角三角形と内心2
⊿ABC は ∠BAC = 90°の直角三角形として
I はその内心とする
D は BC 上の点で CD = CAとする
このとき、次を示せ
① BI は ⊿IDC の外接円に接している
② 四辺形 ABDI は円に内接している
③ AI の延長上に F を
CF = CA であるようにとると
F は ⊿DCI の外接円上にある。
ヒント図
Applet 版
|
|
|
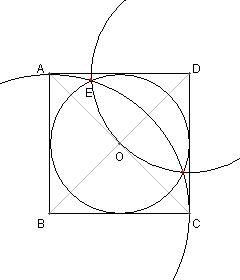
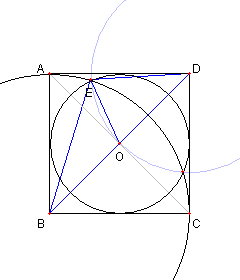
正方形と3つの円
四辺形 ABCD は正方形をなし
O はその中心とするとき
正方形 ABCD の内接円と
円 BA 及び円 DO は
は同一点で交わる
このサイトでは
円 PQ で P を中心とし
半径 PQ の円を表す
ヒント図
Applet 版
|
|
|
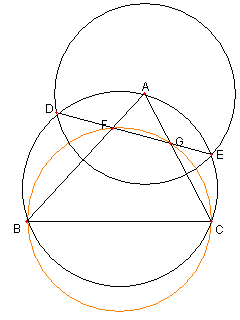
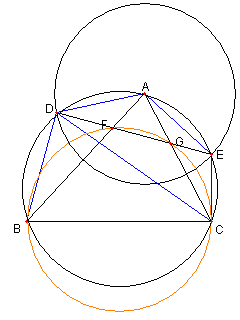
三つの円
図のように
A を中心とする円が
⊿ABC の外接円と
D, E で交わっている
DE と辺 AB, AC との交点を
各々 F, G とする。
このとき、次を示せ
四辺形 BCGF が
円に内接している
ヒント図
Applet 版
|
|
|
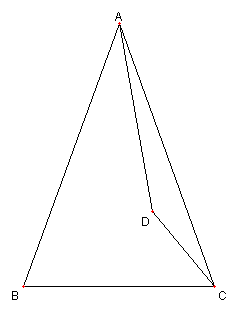
40°の二等辺三角形と角度
⊿ABC は AB = AC, ∠BAC = 40°の
二等辺三角形
D は ⊿ABC 内の点で
AD = BC, ∠DAC = 10°とする。このとき
∠ACD を求めよ
ヒント図
Applet 版
|
|
|
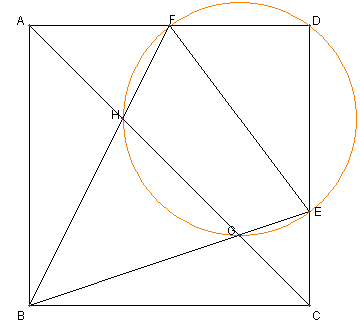
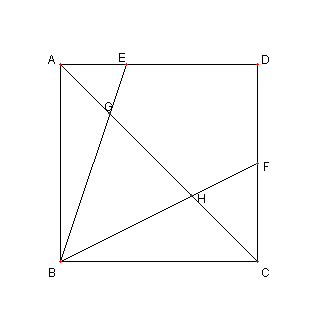
正方形 ABCD において
辺 AD, DC 上に点 E, F を
∠ EBF = 45°となるようにとる
EB, FB と AC との交点を各々 G, H とする。
このとき
GH2 = AG2 + CH2
を示せ
ヒント図
|
|
|
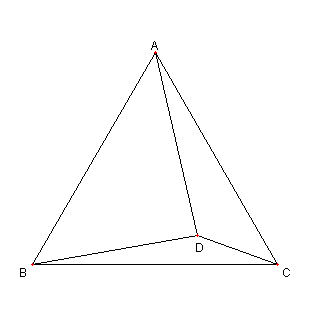
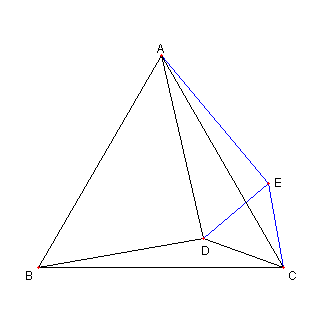
D を正三角形 ABC 内のてんとする。
このとき
AD2 = BP2 + CP2
が成り立つための必要十分条件は
∠BDC = 150°
であることを示せ
ヒント図
|
|
|
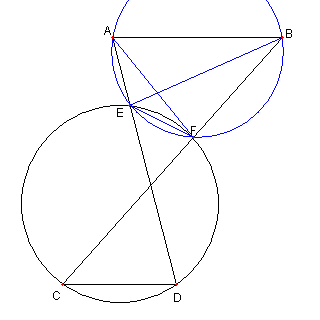
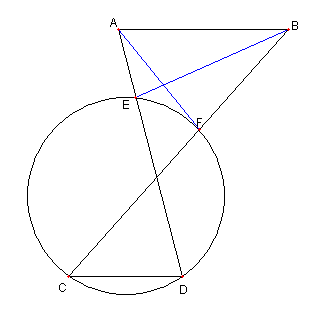
円と平行線
図において C, D, E, F は同一円周上の点
AB と CD は平行線
E は AD 上の点、F はBC 上の点
とする。このとき
∠EAF = ∠EBF を示せ
ヒント図
|
|
|
|
|
|
|
|
|
|
|

|
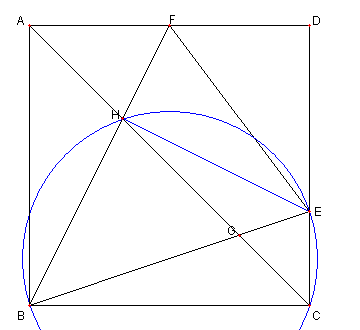
正方形と対角線と 45°
図において
四辺形 ABCD は正方形
E は CD 上の点で、 F は DA 上の点で
∠EBF = 45°とする
このとき、次を示せ。
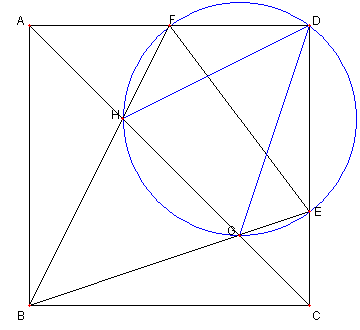
① F, H, G, E, D は EF を直径とする
円の円周上にある。
② EF2 = 2 GH2
③ GH2 = AH2 + CG2
|
|
∠HBE = 45°= ∠HCE より
B, C, H, E は同一円周上にある
故に ∠FHE = ∠BCE = 90°
よって H は EF を直径とする円の円周上にある。
同様に G も EF を直径とする円の円周上にある。
∠EDF = 90°なので
D も EF を直径とする円の円周上にある。
|
|
|
G, H は EF を直径とする円の円周上にある。
D は AC に関して B と対称なので
∠GDH = ∠GBH = 45°である。
よって EF2 = 2 GH2
|
|
|
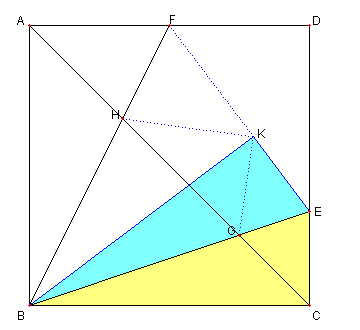
K を BE に関する C の対称点とする。
BK = BC = BA
∠FBK ~ 45°- ∠EBK = 40°- ∠EBC
= ∠FBA
従って
K は BF に関する A の対称点である。
∠EKG = ∠ECG = 45°, ∠FKH = ∠FAH = 45°
よって ∠GKH = 90°
故に GH2 = KH2 + KG2
KH = AH で KG = CG なので
GH2 = AH2 + CG2
K が B から EF に下ろした垂線の足に
なっていることに注意しよう
|
|

|
派生問題
K を B から EF に下ろした垂線の足
M を EK の中点とすると
次が成り立つ。
④ H, G, K, M は同一円周上にある
⑤ GM ∥ CD, HM ∥ AD
戻る
Top に戻る
|
|

|
二つの正方形と二つの直角二等辺三角形
図において
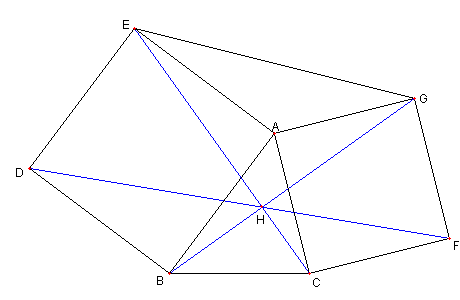
四辺形 ABDE と ACFG は正方形とする。
このとき
EC, DF, BG が一点で交わることを示せ
|
|
|
EC と BG との交点を H とし
∠BHD = ∠GHF を示す。
|
|
|
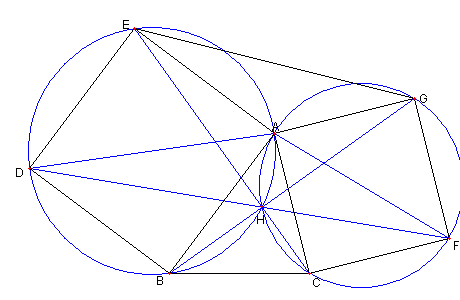
A, E, D, B, H が同一円周上にあり
A, H, C, F, G が同一円周上にあることをみる
∠BHD = ∠BAD = ∠GAF = ∠GHF である
戻る
Top に戻る
|

|
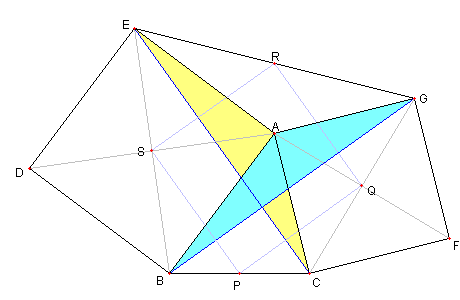
二つの正方形と二つの直角二等辺三角形
図において
四辺形 ABDE と ACFG は正方形とする。
P は BC の中点、R は EG の中点としし
Q は正方形 ACFG の中心、
S は正方形 ABDE の中心とする
このとき
四辺形 PQRS が正方形であることを示せ
|
|
|
⊿AEC ≡ ⊿ABG で
EC と BG が直交している
このことを示し
あとは中点連結定理を使う。
戻る
Top に戻る
|
|

|
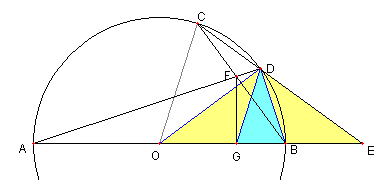
36°72°問題
図において
C, D は O を中心とし
直径 AB の円周上の点で
∠BOD = 36°, ∠BOC = 72°とする。
E は直線 CD と AB との交点、
F は直線 AD と BC との交点、
G は F から AB に下ろした垂線の足とする。
このとき、次を示せ
EG = OB, CD = OG
|
|
|
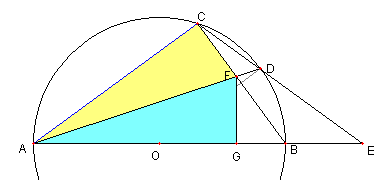
⊿ACF ≡ ⊿AGF を示す。
|
|
|
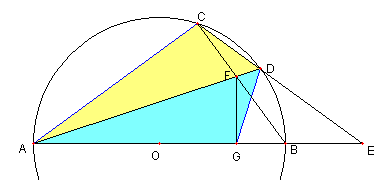
⊿ACD ≡ ⊿AGD を示す。
|
|
|
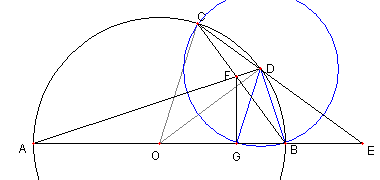
DG = DC = DB をみる。
|
|
|
⊿DOE, ⊿DGB は二等辺三角形である。
|
|
|

|
4つの直角三角形
⊿ABC を ∠BAC = 90°の直角三角形
I を ⊿ABC の内心とする。
D は AB 上の点で ∠AID = 90°
E は BC 上の点で ∠BDE = 90°とする。
このとき
∠EIC = 90°であることを示せ。
|
|
I は ⊿ABC の内心なので
IA, IC は各々
∠BAC, ∠ACB の二等分線である
I を通り AC に平行な直線と
AB, BC 各々おのとの交点を F, G とおく
① AC, FG, DE は平行である
② ∠IAD = 45°, ∠AID = 90°,
∠AFI = 90°なので AF = FD
③ AF = FD なので ① より
CG = GE
④ AC と FC が平行なので
∠GIC = ∠ACI
∠ACI = ∠GCI だったので
∠GIC = ∠GCI
故に GI = GC
⑤ GC = GI = GE より ∠EIC = 90°である。
戻る
Top に戻る
|

|
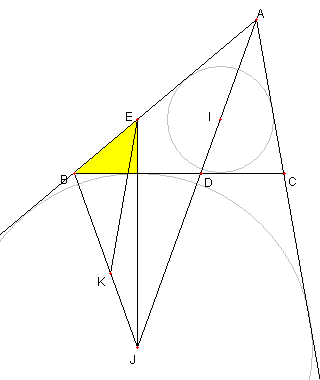
60°,40°,80°の三角形と内心と傍心
⊿ABC は ∠BAC = 60°, ∠ABC = 40°, ∠ACB = 80°
の三角形で I はその内心
J は ∠BAC 内にある傍接円の中心(傍心)
E は J を通り BC に垂直な直線と AB との交点
K は BK = AI なる BJ 上の点とする
このとき、次を示せ。
① I, D, B は E を中心とした円の円周上にある
② B, J, C, I, E は同一円周上にある
③ A, E, K, J は同一円周上にある
|
|
JE と BC が直交し ∠ABC = 40°なので
∠AEJ = 130°である
|
|
|
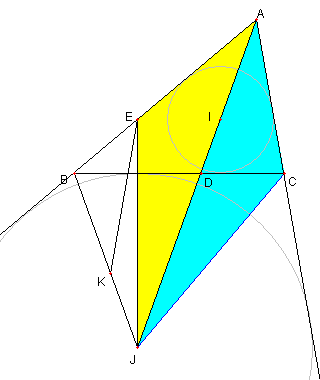
∠ACB = 80°, ∠JCB = 50°より
∠ACJ = 130°である
⊿AEJ と ⊿ACJ において
∠AEJ = 130°= ∠ACJ、∠EAJ = ∠CAJ で
AJ が共通なので
⊿AEJ ≡ ⊿ACJ である
E は AJ に関して C と対称である。
|
|
|
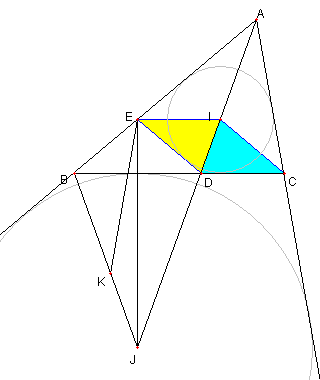
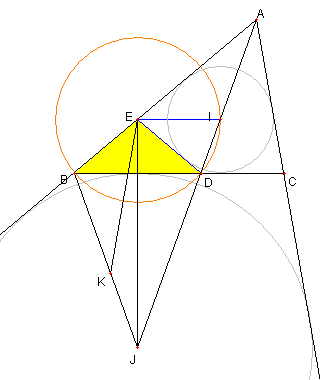
よって ⊿EID ≡ ⊿CID である
∠EID = ∠CID = ∠CAI + ∠ACI = 70°
∠EDI = ∠CDI = 180°- ∠DCA - ∠CAD = 70°
より EI = ED
|
|
|
∠EDB = 180°- ∠EDA - ∠ADC
40°= ∠EBC より
ED = EB
EI = ED だったので ① が示せた
|
|
|
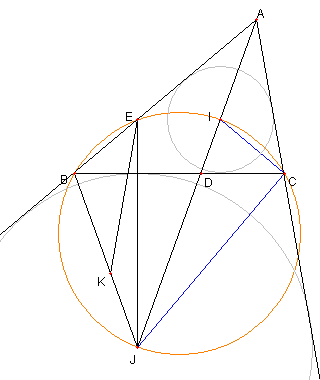
∠CIJ = 70°= ∠CBJ であるので
B, J, C, I は同一円周上にある
∠BEJ = 50°= ∠BCJ であるので
B, J, C, E は同一円周上にある
よって ② が示せた。つまり
B, J, C, I, E は同一円周上にある
|
|
|
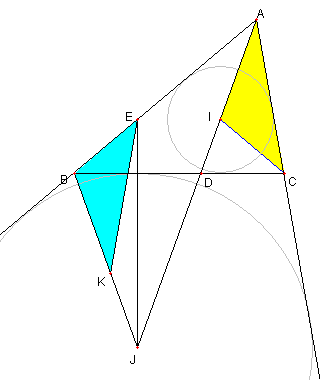
⊿BKE と⊿IAC において
BE = EI = IC
BK = IA
∠EBK = 110°= ∠CIA なので
⊿BKE ≡ ⊿IAC
故に ∠BKE = ∠IAC = 30°である
|
|
|
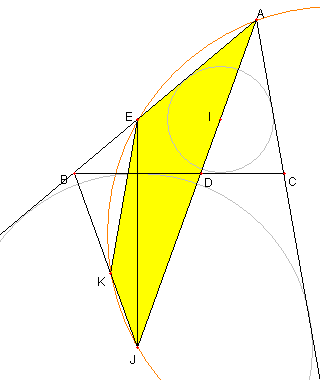
∠BKE = 30°= ∠EAJ なので
A, E, K, J は同一円周上にある。
戻る
Top に戻る
|
|
|

|
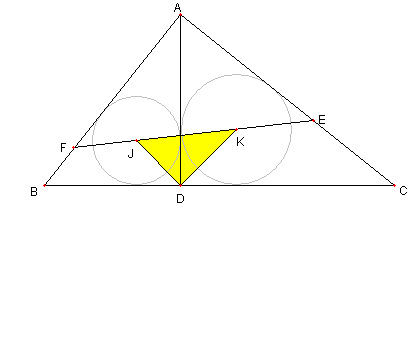
直角三角形と垂線と内心と外接円
⊿ABC は ∠°の直角三角形
D は A から BC に下ろした垂線の足
J, K は各々 ⊿ABD, ⊿ACD の内心
E , F は JK と各々 AC, AB との交点
とする。このとき次を示せ
① 四辺形 DCEK は円に内接する
② 四辺形 BDJF は円に内接する
③ 四辺形 DCEK の外接円
四辺形 BDJF の外接円
⊿AFE の外接円は一点で交わる
|
|
|
⊿DAC ∽ ⊿DJK を示そう
DJ は ∠ADB の二等分線で
DK は ∠ADC の二等分線なので
∠JDK = 90°である。
よって ∠ADC = ∠JDK
⊿DAC ∽ ⊿DBA で相似比が DC : DA より
DK : DJ = DC : DA である。
従って ⊿DAC ∽ ⊿DJK
|
|
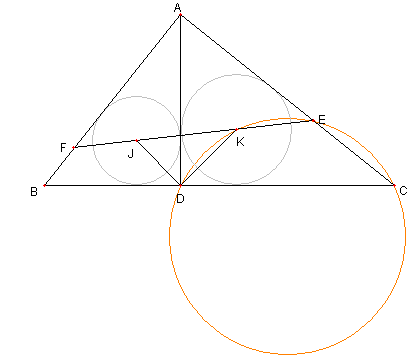
|
⊿DAC ∽ ⊿DJK より
∠ACD = ∠JKD
よって 四辺形 DCEK は円に内接する
① が示せた。同様に ② が示せる。
|
|
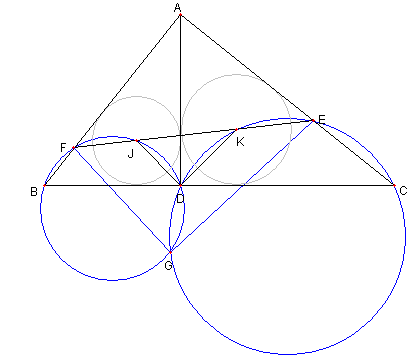
|
四辺形 DCEK の外接円と
四辺形 BDJF の外接円との
D と異なる交点を G とおく。
∠FGE = 90°( = ∠BAC) を示そう。
|
|

|
G の取り方より
∠EGD = ∠DKJ
∠FGD = ∠DJK
また ∠JDK = 90°より
∠DKJ + ∠DJK = 90°である。
よって
∠EGF = ∠EGD + ∠FGD = 90°
∠EAF = 90°だったので
四辺形 AFGE は円に内接している
つまり ⊿AFE の外接円は G を通っている
戻る
Top に戻る
|

|
角度の問題
図において
D, E は各々辺 AB, BC 上の点で
∠DCB = α, ∠ACD = 3α, ∠BAC = 120°- 2α
CE = CA とする。このとき
∠CDE を求めよ。
|
|
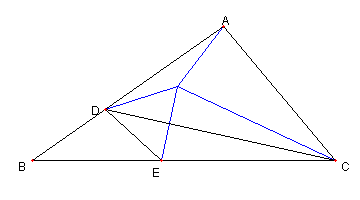
|
題意の図は
相似の意味で一意的に定まるので
答えがわかるように
題意の図を作図しよう
これを、参考にします。
|
|
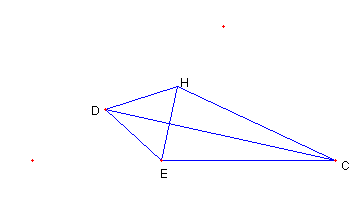
|
正三角形 DEH を画き
D から EH に引いた垂線の
延長線上に点 C を
∠DCE = α (= ∠DCH)
と成るように取る
|
|
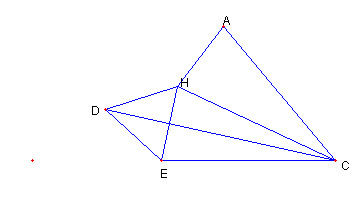
|
CH に関する E の対称点を A とする。
|
|
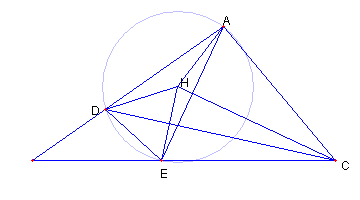
|
AD と CE との交点を B とおく
CA = CE で
∠DCB = α, ∠ACD = 3α である。
∠EAC = 90°- 2α である
HA = HE = ED なので
∠DAE = (∠DHE)/2 = 30°
従って ∠BAC = 90°- 2α
よって、題意の図が描けた。
∠CDE = 30°である。
戻る
Top に戻る
|

|
角度の問題
図において
AB = AC
∠ADB = 55°、∠BDC = 70°
とする。このとき
∠BAC を求めよ。
|
|
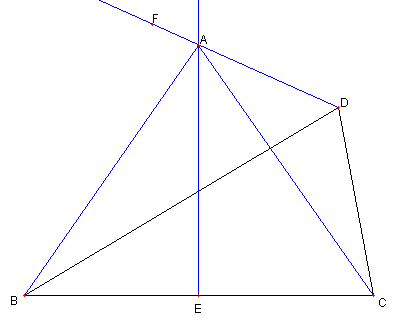
|
図のように F を
∠BDF = 55°となるようにとると
A は BC の垂直二等分線と
DF との交点として定まる。
|
|
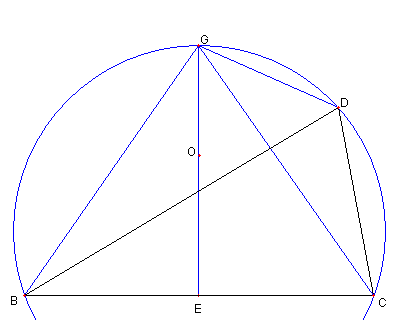
|
O を ⊿BCD の外心とし
E を BC の中心とする
G を ⊿BCD の外接円と
EO の延長との交点とする。
(EO は BC の垂直二等分線である)
|
|
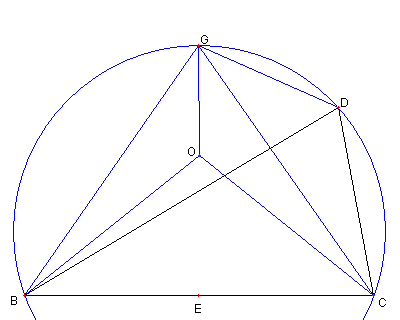
|
∠GOB = ∠GOC で
∠BOC = 2∠BDC = 140°より
∠BOG = 110°である。
故に ∠BDG = (∠BOG)/2 = 55°である
よって G = A であり
∠BAC = (∠BOC)/2 = 70°である
戻る
Top に戻る
|
|

|
角度の問題
図において
AD と BC は平行
∠ABD = 10°、∠DBC = 30°
BA = BC
とする。このとき
∠BDC を求めよ。
|
|
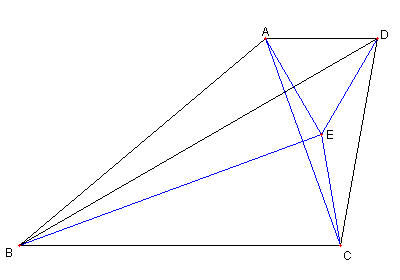
|
図のように点 E を
∠DBE = 10°
BE = BA (= BC) となるようにとる
⊿ABD ≡ ⊿EBD
∠ADB = ∠DBC = 30°
なので ⊿AED は正三角形である
⊿ABE ≡ ⊿CBE
なので EA = EC
ED = EA だったので
E は ⊿ACD の外接円の中心である。
∠ADC = (∠AEC)/2 = ∠AEB = 80° で
∠ADB = 30°なので
∠BDC = 50°である。
戻る
Top に戻る
|
|

|
⊿IBE の外接円と
⊿IDC の外接円との交点を
G とする( I 以外)。
∠IGC = ∠IDC = ∠IAC = 45°
∠IGB = ∠IEB = ∠IAB = 45°なので
∠BGC = 90°である
∠BAC = 90°だったので
G は ⊿ABC の外接円上にある。
戻る
Top に戻る
|
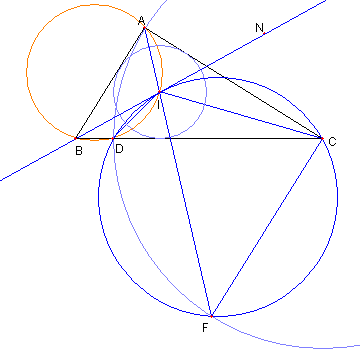
|
IC が ∠ACB の二等分線で
CD = CA なので
∠IBD = ∠IAC = 45°= ∠IAB
なので ② が示せる。
IB も ∠ABC の二等分で
∠ABC + ∠ACB = 90°なので
∠IBC + ∠ICB = 45°
つまり、図において
∠CIN = 45°= ∠IDC
よって ① が示せる。
CF = CA より
∠CFA = ∠CAF = 45°= ∠CDI
よって ③ が示せる
戻る
Top に戻る
|

|
40°の二等辺三角形と角度
⊿ABC は AB = AC,
∠BAC = 40°の
二等辺三角形
D は ⊿ABC 内の点で
AD = BC, ∠DAC = 10°とする。
このとき
∠ACD を求めよ
|
|
|
題意の図は相似の意味で
一意的に定まる。
答えがわかるように、
題意の図を画く
ことにする。
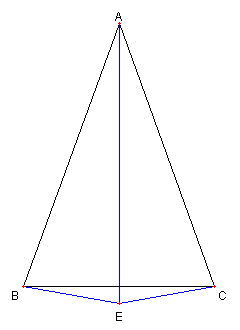
図のように
E を AE = AB (= AC)
∠BAE = 20°(= ∠EAC)
となるように描く
EB = EC,∠BCE = 10°
である。
|
|
|
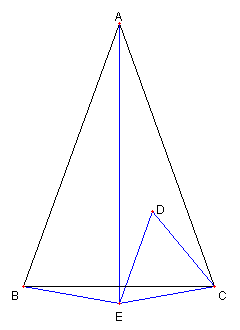
図のように
正三角形 DEC を画く
|
|
|
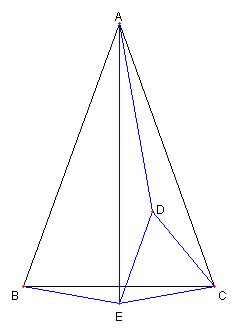
∠DAC = 10°, ∠ACD = 20°
である。
|
|
|
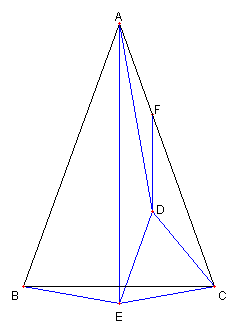
図のように
AC 上に点 F を
∠DFC = 20°( = ∠DCF)
となるようにとる
∠DAF = 10°= ∠ADF である。
FA = FD = DC = EC である。
⊿FAD ≡ ⊿ECB
を得て AD = BC を得る。
題意の図が描けて
∠ACD = 20°である
戻る
Top に戻る
|
|
|
E を 正方形 ABCD の
内接円と円 BA との
交点の一つとする
DE = DO を示す
O は BD の中点なので
EB2 + ED2
= 2(EO2 + BO2)
これより DE = DO を得る
戻る
Top に戻る
|
|
|
∠AFG = ∠ADE + ∠DAB
∠ADE = ∠AED = ∠ACD
∠DAB = ∠DCB
∠GCB = ∠ACD + ∠DCB
なので
∠AFG = ∠GCB
従って、四辺形 BCGF は
円に内接している
戻る
Top に戻る
|
|
|
|
⊿EDC が正三角形なる点 E をとり
⊿AEC ≡ ⊿BDC に注目する
戻る
Top に戻る
|
|
|