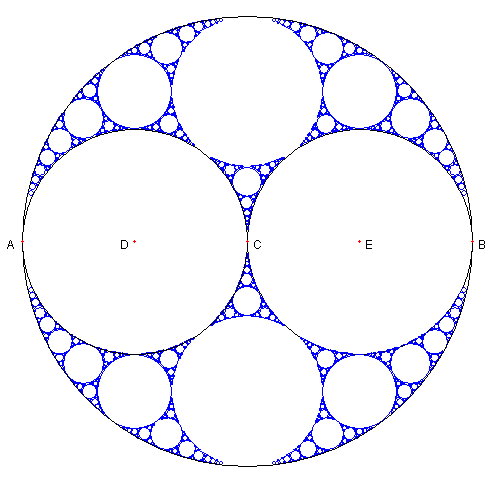
直径1の円に
接し互いに接している直径 1/2 の円を画く
三つの円に接している円を2つ描く
順に接している円を画いて左の図をえる
問題
ここに登場するするすべての円の直径は
整数分の1 である。
図の構成 図の描き方 問題の解説

|
西田の円 直径1の円に 接し互いに接している直径 1/2 の円を画く 三つの円に接している円を2つ描く 順に接している円を画いて左の図をえる 問題 ここに登場するするすべての円の直径は 整数分の1 である。 図の構成 図の描き方 問題の解説 |
|
|
| ||||||
|
|
| ||||||
|
|
|
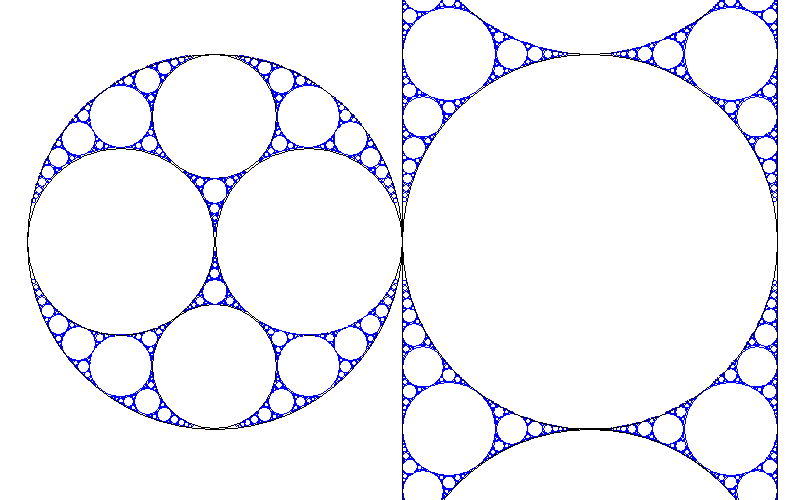
| 反転を利用して描きます |
|
| ||||||||
|
一般に円 C 内にあり円 D 外にあるの円 K* に対して その反転を M* とする。 M* を上方に 1 (AB の長さ)だけ平行移動した円を M*1 とおく M*1 の反転を K*1 とおく C を通り AB と垂直な直線に対して K*1 と対称な円を K*2 とおく K*2 の反転を M*2 とおく 平行な二直線の真ん中の線に対して M*2 と対称な円を M*3 とおき M*3 の反転を K*3 とおく K*1, K*2, K*3 を K* の子という M*1, M*2, M*3 を M* の子という M* は K* の反転 M*1 は M* を上方 1 平行移動したもの K*1 は M*1 の反転 K*2 は K*1 の対称円 (円内での) M*2 は K*2 の反転 M*3 は M*2 の対称円 (平行二直線内での) K*3 は M*3 の反転 | ||||||||
|
| ||||||||
|
|
|
(p,q) を 円 P の点なので (p-a)2 + (q-b)2 = r2 である。 よって 2ap + 2bq = p2 + q2 + a2 + b2 - r2 = m + s である。 ((p/m - a/s)2 + (q/m - b/s)2 - (r/s)2) (sm)2 = (sp-am)2 + (sq - bm)2 - (rm)2 = s2(p2+q2) - 2sm(ap + bq) + m2(a2 + b2 - r2) = s2m - sm(m + s) + m2s = 0 なので (p/m - a/s)2 + (q/m - b/s)2 - (r/s)2 = 0 (a,b) を中心とし半径 r の円の反転は s = a2 + b2 - r2 とし s > 0 のとき (a/s, b/s) を中心とし半径 r/s の円である。 この互いに反転となっている二つの円に対して (1/r, a/r,b/r,s/r) を考える。 (a/r)2 + (b/r)2 = (a2 + b2)/r2 = (r2 + s)/r2 = 1 + (1/r)(s/r) に注意しておこう | ||
|
V = {(α, β, γ, δ)|α, β, γ, δ は実数で、α > 0, δ > 0, β2 + γ2 =
1 + αδ} とおく。 (α, β, γ, δ) が V の元のとき r = 1/α, a = β/α = rβ, b = γ/α = rγ とおき s = a2 + b2 - r2 とおくとき s = r2(β2 + γ2 - 1) = r2αδ = rδ となり r/s = 1/δ, a/s = β/δ, b/s = γ/δ になる。 |
以上の議論より (α, β, γ, δ) が V の元のとき (β/α,γ/α) を中心として半径 1/α の円の反転は (β/δ,γ/δ) を中心として半径 1/δ の円である | ||
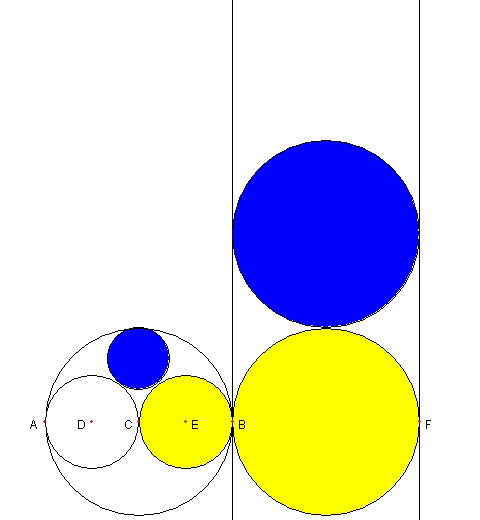
|
左の図において 円 C 内の黄色の円は 中心が (3/4,0) で半径が 1/4 の円である (3/4)2 + 02 - (1/4)2 = 1/2 (1/2)/(1/4) = 2, (3/4)/(1/4) = 3 である。 黄色い二つの円に対応するデータは (4,3,0,2) である。 大きいほうの黄色い円はこのデータより 中心が (3/2,0) で半径が 1/2 の円である。 円 M は大きい黄色の円を上方に 1 だけ平行移動したものなので それは (3/2,1) で半径 1/2 の円である。 (3/2)2 + 12 - (1/2)2 = 3 3/(1/2) = 6, (3/2)/(1/2) = 3, 1/(1/2) = 2 なので 円内の青い円 K 及び M に対応するデータは (6,3,2,2) である。 K は (1/2,1/3) を中心とし半径 1/6 の円である。 W = {(α, β, γ, δ) ∈ V|α, β, γ, δ は 整数で、α , δ は正の偶数とする} とおく。 K と M に対応するデータは W に属している | ||
|
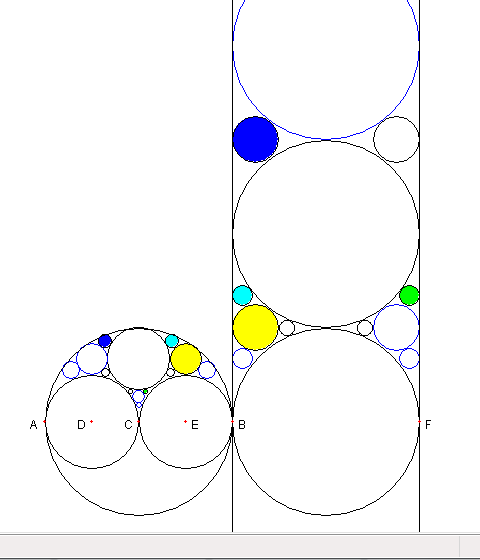
次を示す。 円 K* とその反転円 M* を考える K*1 と M*1 のデータは W に属する ② K*1 と M*1 のデータが W に属するとき K*2 と M*2 のデータは W に属する ③ K*2 と M*2 のデータが W に属するとき K*3 と M*3 のデータは W に属する ① の証明 円 K* とその反転円 M* に対応するデータを (α, β, γ, δ) として、それが W に属しているとする。 β2 + γ2 = 1 + αδ である。 M* は中心が (β/δ,γ/δ) で半径が 1/δ の円である M*1 は M* を上方に 1 平行移動したものなので M*1 は中心が (β/δ,γ/δ + 1) で半径が 1/δ の円である (β/δ)2 + (γ/δ + 1)2 - (1/γ/δ)2 = α/δ+1+2γ/δ (α/δ+1+2γ/δ)/(1/δ) = α + δ + 2γ なので K*1 と M*1 に対応するデータは ( α + δ + 2γ, β, γ + δδ) これは W に属している。 ② の証明 円 K*1 とその反転円 M*1 に対応するデータを (α, β, γ, δ) として、それが W に属しているとする。 β2 + γ2 = 1 + αδ である。 K*1 は中心が (β/α,γ/α) で 半径 1/α の円である 従って K*2 は中心が (1-β/α,γ/α) で 半径 1/α の円である (1-β/α)2 + (γ/α)2 - (1/α)2 = δ/α + 1 - 2β/α (δ/α + 1 - 2β/α)/(1/α) = δ + α - 2β なので K*2 と M*2 に対応するデータは (α, α - β,γ,δ + α - 2β) で、これは W に属している | ||

|
③ の証明 円 K*2 とその反転円 M*2 に対応するデータを (α, β, γ, δ) として、それが W に属しているとする。 β2 + γ2 = 1 + αδ である。 M*2 は中心が (β/δ,γ/δ) で半径が 1/δ の円である M*3 の定義より M*3 は中心が (3-β/δ,γ/δ) で半径が 1/δ の円である (3-β/δ)2 + (γ/δ)2 - (1/δ)2 = α/δ + 9 - 6β/δ (α/δ+9-6β/δ)/(1/δ) = α + 9δ - 6β なので K*3 と M*3 に対応するデータは ( α + 9δ - 6β ,3δ - β, γ, δ) これは W に属している。 以上より次のことがわかる。 K と M の子孫に対応するデータは W に属している。 従って K*, M* を K, M の子孫の円とすると K* の半径は 1/偶数であり直径は 1/整数である 図の構成 図の描き方 解説 Top に行く |
|
| ||||||||||||||||||||||
|
| ||||||||||||||||||||||
|
| ||||||||||||||||||||||
|
|