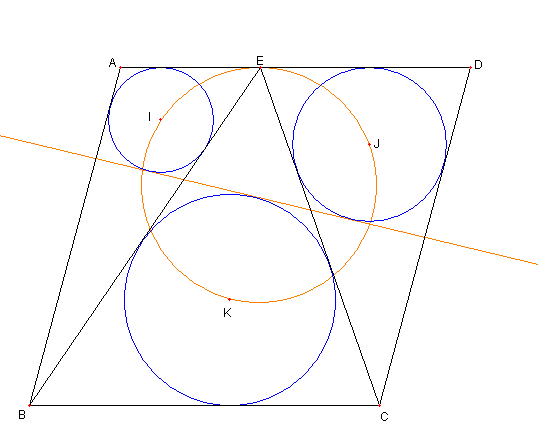
図において
四辺形 ABCD は菱形で
E は辺 AD 上の点とする
I, J, K は各々
僊BE, 僞CD, 僞BC の内心とする
このとき
@ 三つの内接円に接する直線がある
A 四辺形 EIKJ は円に内接している
@ は Go Geometry にあった問題です
A は @ を使えば示せます。
Go Geometry にもありますが
四辺形 ABCD は菱形でなく、一般的に
円に外接する四辺形にとして
@ は成り立ちます
A も成り立ちます
証明は一般論で行います
一般論へ
|
|
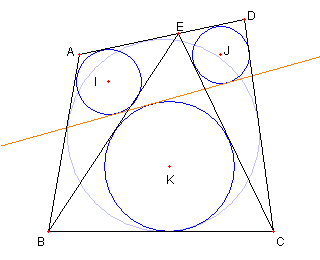
菱形と内心と外接円 図において 四辺形 ABCD は菱形で E は辺 AD 上の点とする I, J, K は各々 僊BE, 僞CD, 僞BC の内心とする このとき @ 三つの内接円に接する直線がある A 四辺形 EIKJ は円に内接している @ は Go Geometry にあった問題です A は @ を使えば示せます。 Go Geometry にもありますが 四辺形 ABCD は菱形でなく、一般的に 円に外接する四辺形にとして @ は成り立ちます A も成り立ちます 証明は一般論で行います 一般論へ |
|
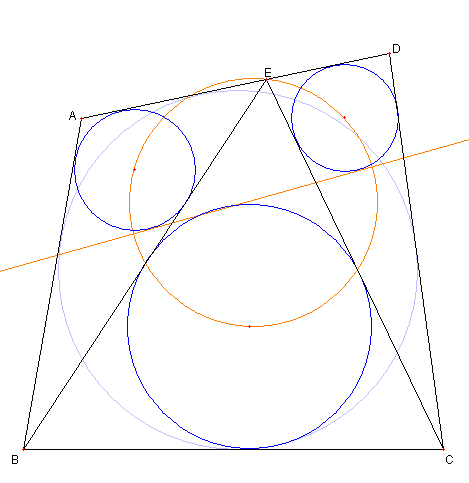
円に外接する四辺形と内心と外接円 図において 四辺形 ABCD は円に外接する四辺形で E は辺 AD 上の点とする I, J, K は各々 僊BE, 僞CD, 僞BC の内心とする このとき @ 三つの内接円に接する直線がある A 四辺形 EIKJ は円に内接している 問題の説明 @の証明 Aの証明 Top に戻る |
|
|
|
|
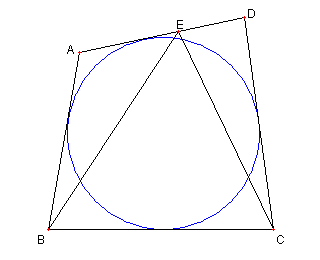
円に内接している四辺形 ABCD の 辺 AD 上に点 E をとる |
僊BE, 僞CD, 僞BC の内接円 I, J, K を描く このとき |
@ 三つの内接円 I, J, K に接する直線がある。 A 四辺形 EIKJ は円に内接している @の証明 Aの証明 Top に戻る |
|
|
|
|
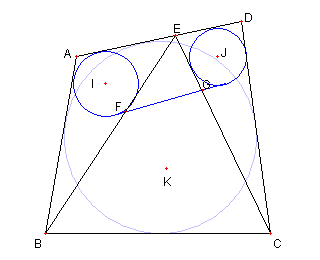
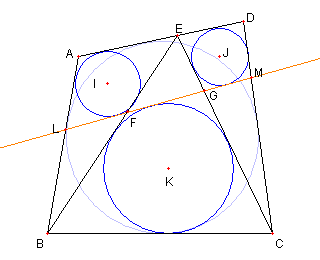
図のように円 I と円 J の共通接線と EB, EC との交点を各々 F, G とおく 四辺形 FBCG が円に外接していることを示す そのために B FG + BC = FB + GC を示す これが示されれば 四辺形 FBCG が 円に内接することがわかる |
円 I と直線 AB, BE, EA, FG との接点を 各々 S, U, L, P とし 円 J と直線 DC, CE, ED, PG との接点を 各々 T, V, M, Q とする。 このとき |
(1) AB + CD = AD + BC (2) AS = AL, DT = DM より (3) SB + TC = LM + BC さらに (4) SB = UB, TC = VC, LM = PQ より (5) UB + VC = PQ + BC 次に (6) UF = PF, VG = QG なので FB + GC = FG + BC が成り立つ 問題の説明 Aの証明 Top に戻る |
|
|
|
|
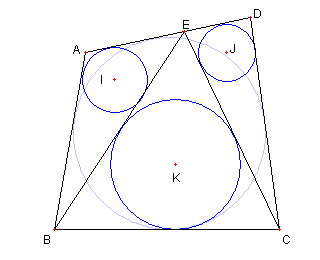
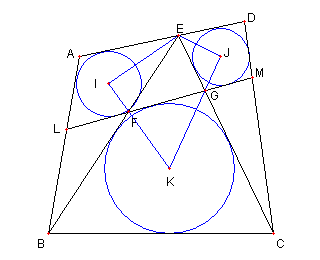
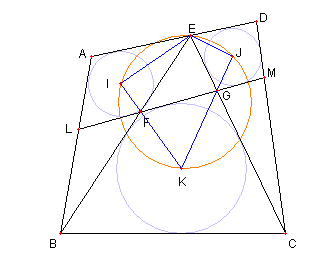
今までの記号を変えて説明します A, B, C, D, E, I, J, K は 今までと同じとし 円 I, J, K の共通接線と 直線 EB, EC, AB, DC との交点を 各々 F, G, L, M とする |
F が線分 IK 上にあり, G が線分 JK 上にあって ∠EFI = ∠LFI, ∠EGJ = ∠MGI さらに ∠AEI = ∠FEI, ∠DEJ = ∠GEJ であることに注意しよう。 |
∠AEF + ∠EFL + ∠DEG + ∠EGM = 360° なので ∠IEF + ∠EFI + ∠JEG + ∠EGJ = 180° 従って ∠EIF + ∠EJG = 180° つまり ∠EIK + ∠EJK = 180° なので 四辺形 EIKJ は円に内接している 問題の説明 @の証明 Top に戻る |