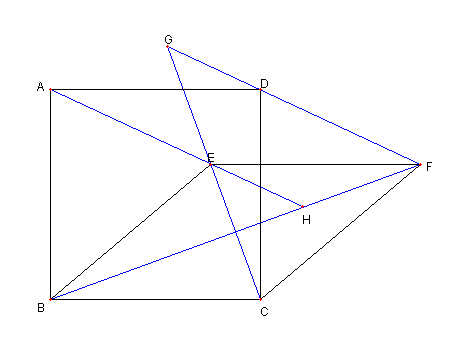
図において
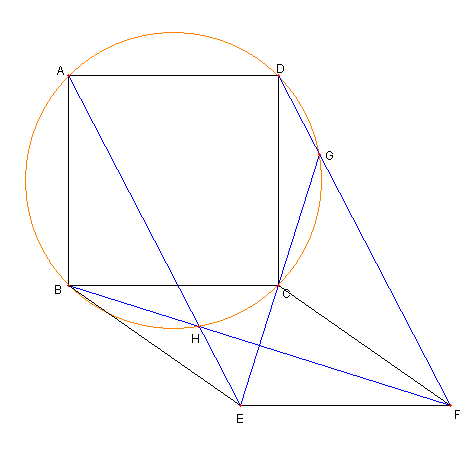
四辺形 ABCD は正方形で
四辺形 EBCF は菱形とする
G は直線 CE と FD の交点
H は直線 AE と BF の交点
とする
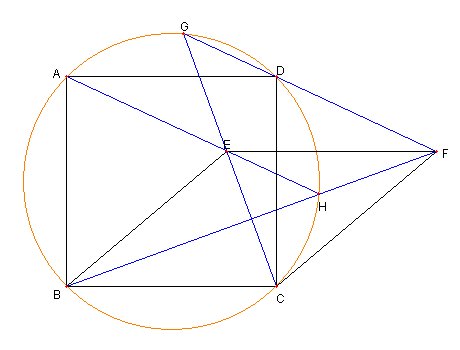
G, H は正方形 ABCD の
外接円の円周上にある
問題1の略解答 問題3、4 まとめ問題
このとき
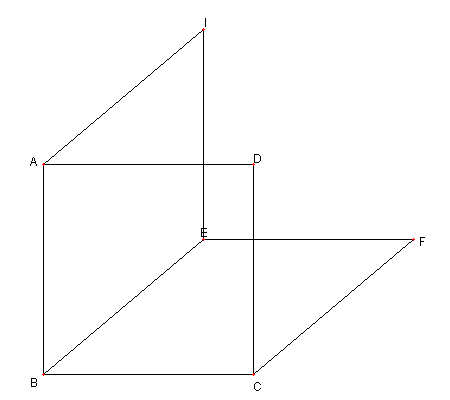
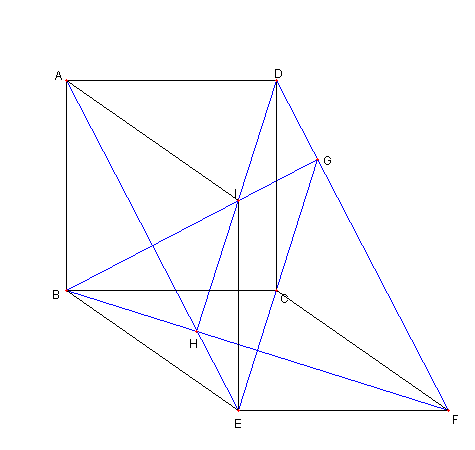
BI, CE, FD は一点で交わり
AE, BF, ID は一点で交わる
問題2の解答へ
菱形がこちらでも成り立つ
問題3の略解答
菱形がこちらでも成り立つ
問題4の略解答 Top に戻る

|

|
|
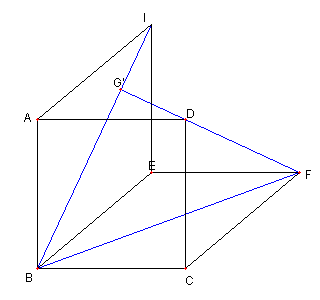
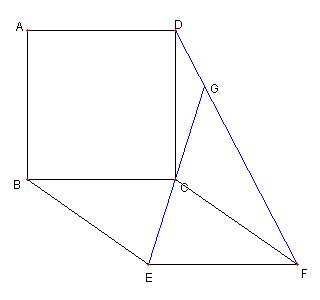
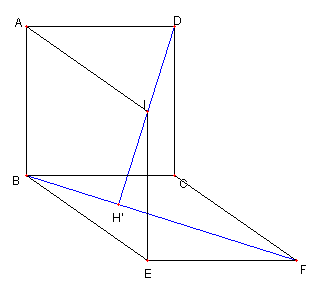
正方形と菱形と外接円 図において 四辺形 ABCD は正方形で 四辺形 EBCF は菱形とする G は直線 CE と FD の交点 H は直線 AE と BF の交点 とする |
問題1 G, H は正方形 ABCD の 外接円の円周上にある 問題1の略解答 問題3、4 まとめ問題 |

|

|
|
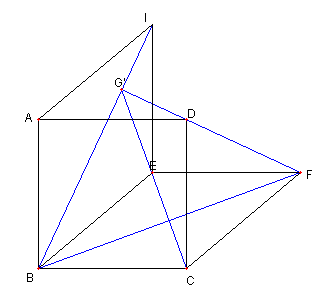
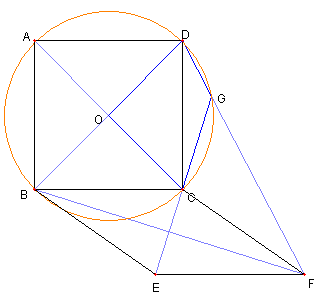
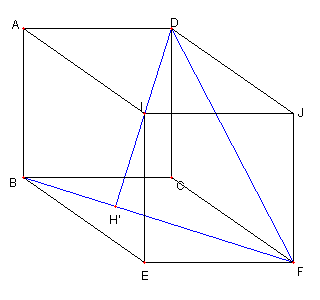
更に菱形 ABEI を描く このとき |
問題2 BI, CE, FD は一点で交わり AE, BF, ID は一点で交わる 問題2の解答へ |

|

|
|
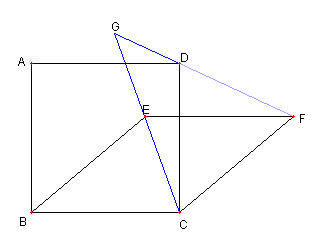
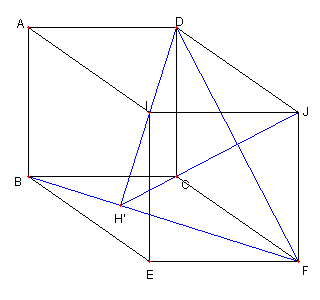
問題3 菱形がこちらでも成り立つ 問題3の略解答 |
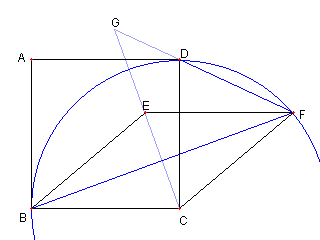
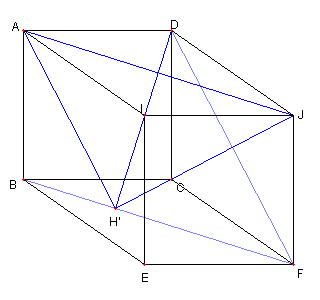
問題4 菱形がこちらでも成り立つ 問題4の略解答 Top に戻る |
|
|
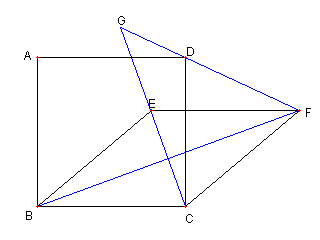
|
| ∠CGD = 45°を示す |
B, D, F は C を中心とする円周上にあり ∠BCD = 90°なので ∠BFD = 45°である |
CE と BF が直交し ∠BFD = 45°なので ∠CGF = 45°である |
|
|
|
|
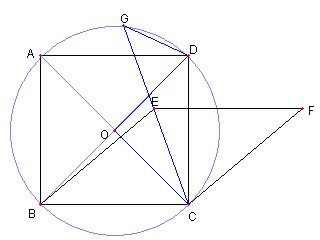
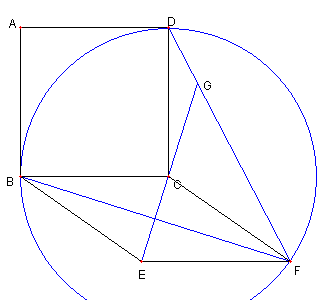
正方形 ABCD はその中心 O を 中心とする円に内接し ∠COD = 90°, ∠CGD = 45°なので G もその円の円周上にある。 |
A, E, C は B を中心とする円上にあり ∠ABC = 90°なので ∠AEC = 135°である。 |
CE と BF が直交し ∠AEC = 135°なので ∠AHB = 45°である。よって H は正方形 ABCD の外接円上にある Top に戻る |
|
|
|
|
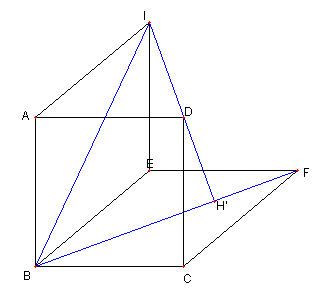
直線 FD と BI との交点を G' とおく G = G' を示す ∠ABC = 90°であり BI が ∠ABE の二等分線で BF が ∠CBE の二等分線なので ∠FBI = 45°である。 CB = CD = CF で ∠BCD = 90°より ∠BFD = 45°である。 |
∠G'BF = 45°= ∠G'FB より G'B = G'F である。 EB = EF なので G'E は BF を垂直二等分する よって、直線 G'E は C を通る。 ゆえに、G = G' である |
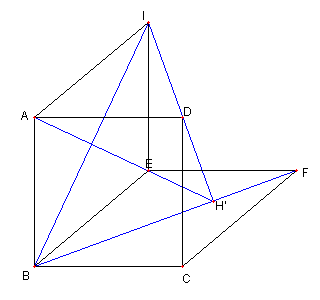
直線 ID と BF との交点を H' とおく ∠H'BI = 45°= ∠H'IB |
| ||
|
H'A = H'I, EA = EI に注目して 直線 H'E が A を通ることをみて H = H' を得る Top に戻る |
|
|
|
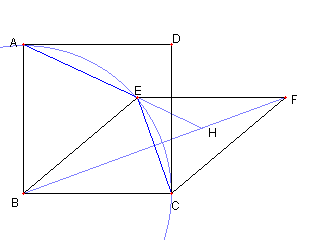
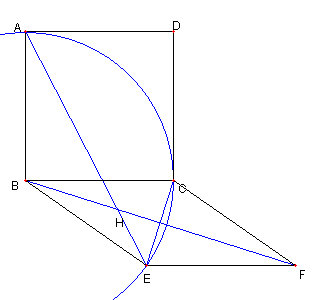
| ∠CGD = 135°を示す |
B, D, F は C を中心とする円周上にあり ∠BCD = 90°なので ∠BFD = 45°である |
CE と BF が直交し ∠BFD = 45°なので ∠CGD = 135°である |
|
|
|
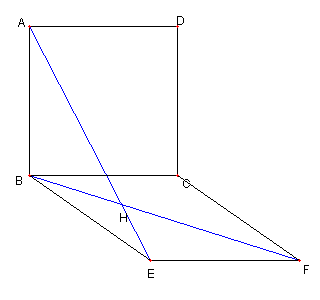
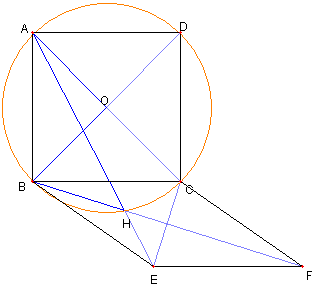
| ∠AHB = 45°を示す |
A, E, C は B を中心とする円上にあり ∠ABC = 90°なので ∠AEC = 45°である。 CE と BF が直交しているので ∠AHB = 45°である |
∠AHB = 45°なので H は正方形 ABCD の外接円周上にある Top に戻る |
|
|
|
|
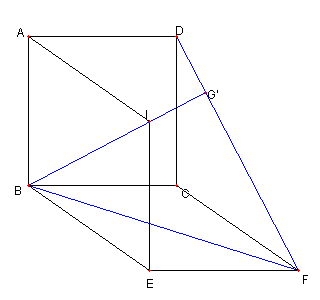
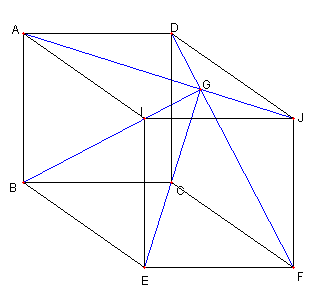
直線 DF と BI との交点を G' とする G = G' 即ち、 G' が直線 EC 上にある ことを示す |
BI が ∠ABE の二等分線 BF が ∠CBE の二等分線 ∠ABC = 90°なので ∠G'BF = 45°である。 CB = CD = CF で ∠BCD = 90°なので ∠G'FB = 45°である。 ゆえに G'B = G'F である。 CB = CF, EB = EF なので G', C, E は一直線上にある。 |
直線 BF と DI との交点を H' とおく H = H' を示す つまり、H' が AE 上にあることを示す。 そのために AH が ∠BAI の二等分線であることを示す |
|
|
|
|
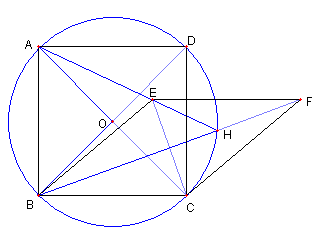
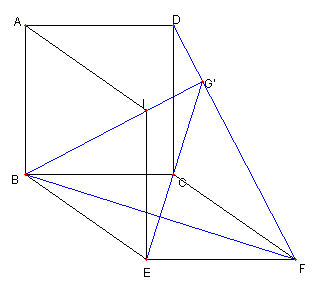
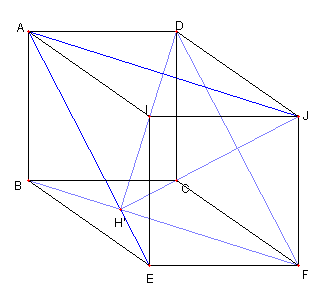
図のように、菱形 DCFJ を描く DI が ∠ADJ の二等分線 DF が ∠CDJ の二等分線 ∠ADC = 90°なので ∠H'DF = 45°である。 CB = CD = CF で ∠BCD = 90°なので ∠BFD = 45°である。 |
∠H'DF = 45°= ∠H'FD なので H'D = H'F さらに CD = CF, JD = JF なので H', C, J は一直線上にある |
JC が ∠DJF の二等分線 JA が ∠DJI の二等分線 ∠ADC = 90°なので ∠H'JA = 45°である。 DI は AJ の垂直二等分線であるので ∠H'AJ = ∠H'JA = 45° |
|
|
|
|
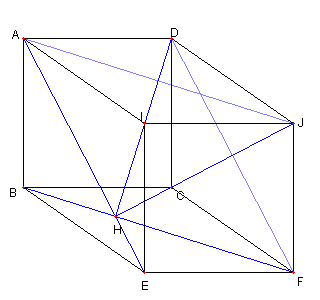
∠H'AJ = 45°で AJ が ∠DAI の二等分線で ∠BAD = 90°なので H'A は ∠BAI の二等分線である。 |
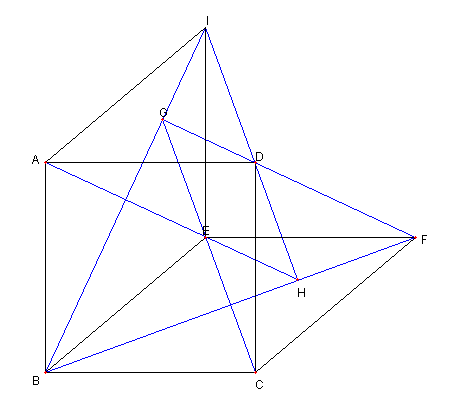
今までの結果より 4直線 AE, BF, CJ, DI は 一点で交わる |
同様に 4直線 AJ, BI, CE, DF は 一点で交わる Top に戻る |
|
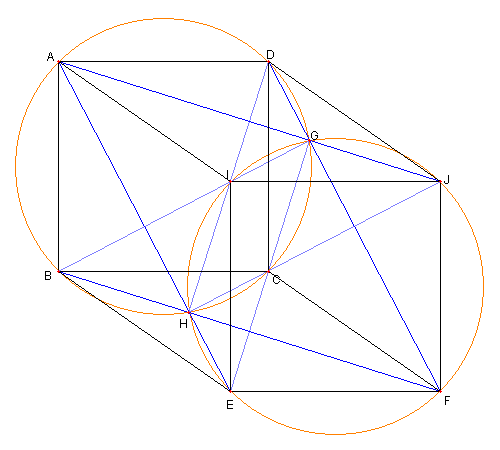
今までを総合すると 次が成り立つ 四辺形 ABCD は正方形で 四辺形 ABEI は菱形で 四辺形 IEFJ は正方形であるとする AJ と DF との交点を G AE と BF との交点を H とするとき ① A, B, H, C, G, D は同一円周上にある ② I, H, E, F, J, G は同一円周上にある ③ 直線 BI と CE は G を通る ④ 直線 DI と CJ は H を通る Top に戻る |