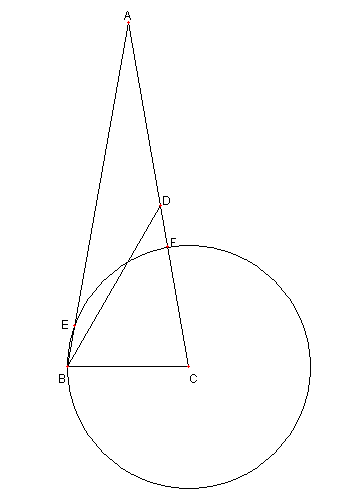
⊿ABC は
∠BAC = 20°, AB = AC
の二等辺三角形である。
D は AC 上の点で DA = DB とする。
C を中心とし半径 CB の円と
AB, AC の交点 E, F を
図のようにとるとき
BE = DF である。
このサイトでは
C を中心とし半径 CB の円を
円 CB という
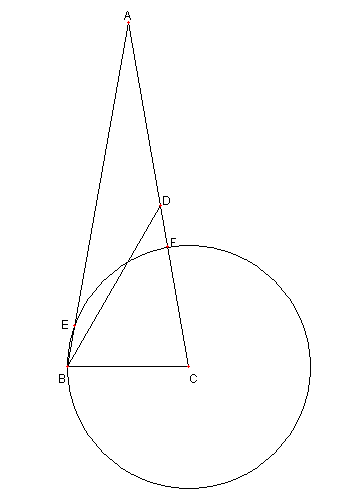
|
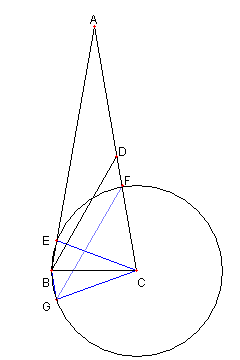
問題 ⊿ABC は ∠BAC = 20°, AB = AC の二等辺三角形である。 D は AC 上の点で DA = DB とする。 C を中心とし半径 CB の円と AB, AC の交点 E, F を 図のようにとるとき BE = DF である。 このサイトでは C を中心とし半径 CB の円を 円 CB という |
|
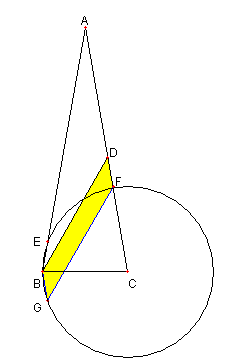
|
|
|
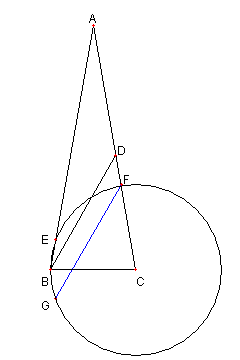
F を通り DB と平行な直線が 円 CB と再び交わる点を G とおく |
四辺形 BGFD が平行四辺形 であることを示す |
GB = BE に注意する。 Top に戻る |