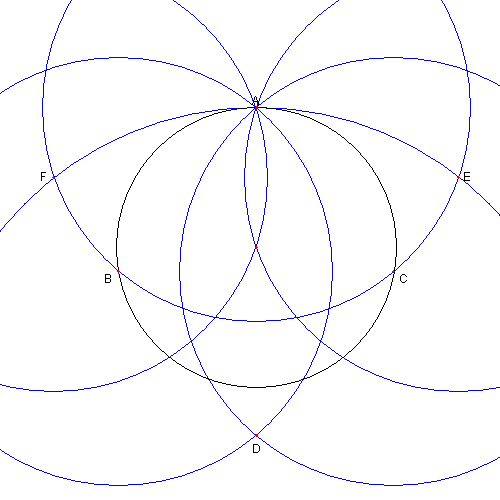
コンパスのみを使って
その中心を作図する
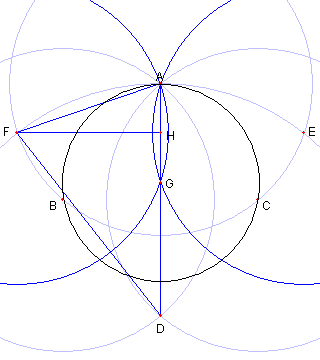
左がその作図の様子である。
作図の手順を示し
それが、それでよいことを示すのを
問題にします。
手順 解答
Go Geometry にあった問題です

|
円があたえられたとき コンパスのみを使って その中心を作図する 左がその作図の様子である。 作図の手順を示し それが、それでよいことを示すのを 問題にします。 手順 解答 Go Geometry にあった問題です |

|
|
|
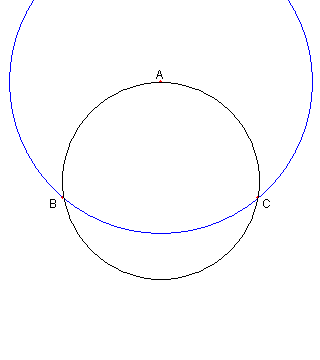
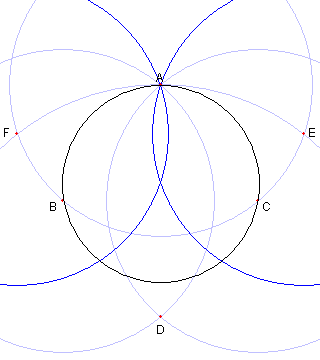
| この円の中心を作図する |
与えられた円上に点 A をとり A を中心とし、もとの円と B, C で交わる円を描く |
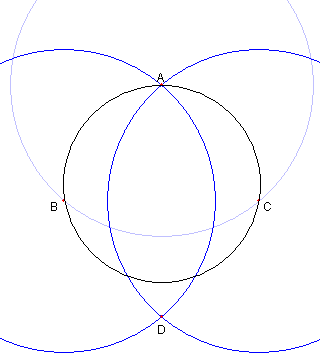
二円 BA と CA の もう一方の交点を D とする。 このサイトでは B を中心とし C を通る円を 円 BC という |
|
| |
|
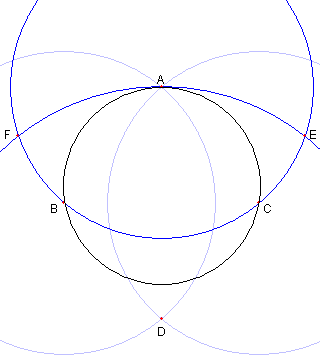
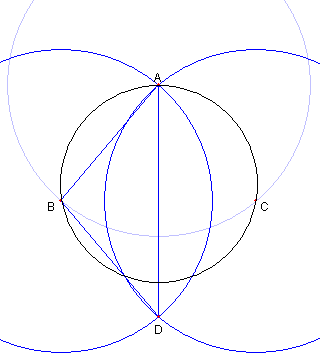
円 AB と円 DA の交点を E, F とおく |
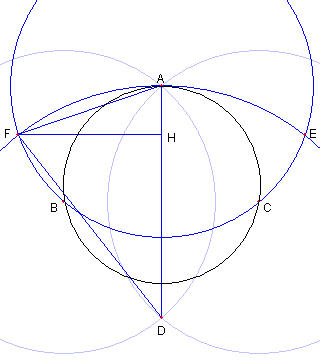
二円 EA と FA の もう一方の交点を G とする。 G ば求める中心である | Top に戻る 解答 |
|
|
|
|
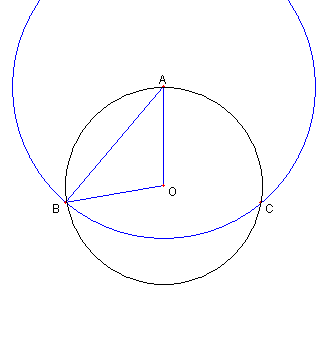
与えられた円の中心を O とし 半径を 1 とする。 θ = ∠BAO とおくと AB = 2 cos θ |
AD = 2 AB cos θ = 4(cos θ)2 |
F から AH に下ろした垂線の足を H とおく FD = AD = 4(cos θ)2 FA = AB = 2 cos θ である。 |

|
| |
|
(DH - AH)×AD = DH2 - AH2 = FD2 - FA2 = (4(cos θ)2)2 - (2 cos θ)2 = 4(cos θ)2(4(cos θ)2)-1) = AD×(AD - 1) |
よって DH - HA = AD - 1 AD = DH - HA なので AH = 1/2 |
G を円 EA と FA との もう一つの交点とすると 図形の対称性より 元との円の中心 O や G は 半直線 AD の上にあり H は AG の中点である AH = 1/2 より AG = 1 よって G = O である。 |