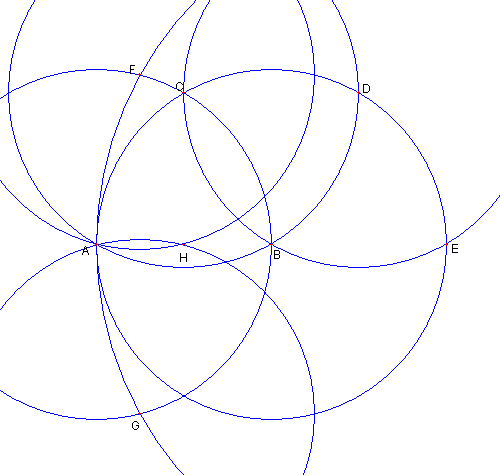
コンパスのみを使って
その中心を作図する作図法である
左がその作図の様子である。
作図の手順を示し
それが、それでよいことを示すのを
問題にします。
手順 解答
京都府の数学コンテストに
出題された問題です

|
二点 A, B が与えられているとき コンパスのみを使って その中心を作図する作図法である 左がその作図の様子である。 作図の手順を示し それが、それでよいことを示すのを 問題にします。 手順 解答 京都府の数学コンテストに 出題された問題です |
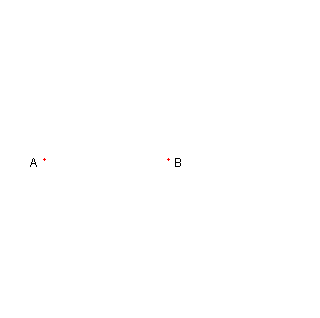
|
|
|
|
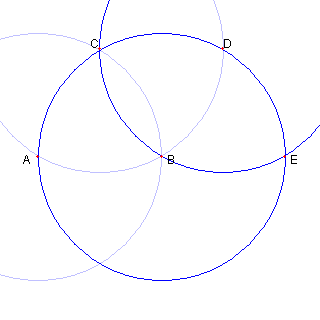
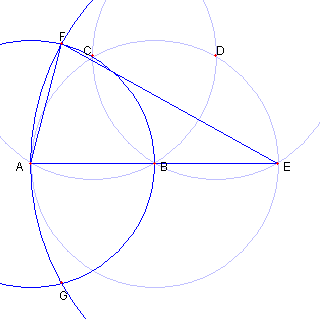
二点 A, B が与えられている |
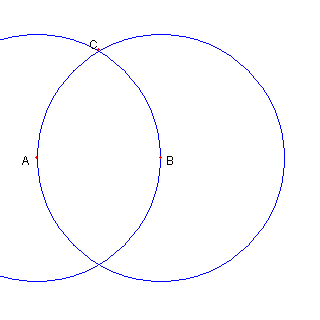
円 AB と円 BA との交点の一つを C とする |
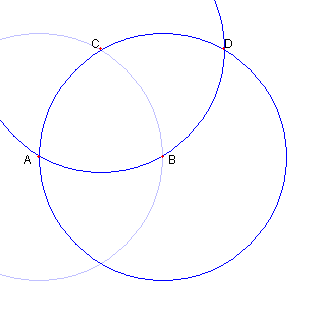
円 BA と円 CA との もう一つの交点を D とする |
|
|
|
|
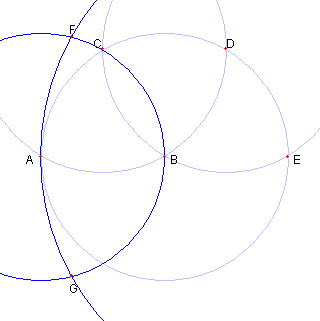
円 BA と円 DB との もう一つの交点を E とする |
円 AB と円 EA との 交点を F, G とする |
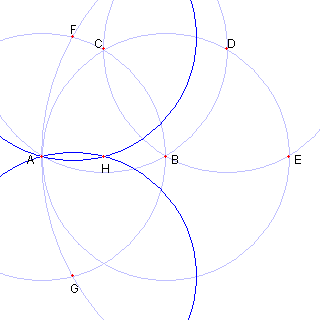
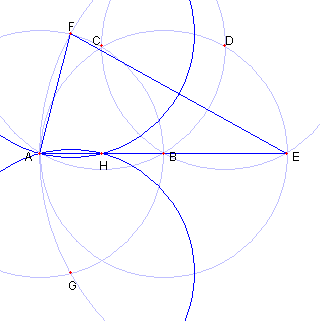
もう一つの交点を H とする H が求める点である。 Top に戻る 解答 |
|
|
|
|
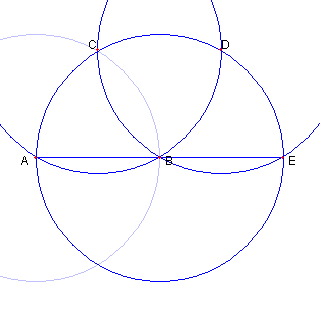
AB の長さを 1 とする。 AE は円 BA の直径となり 長さは 2 である。 |
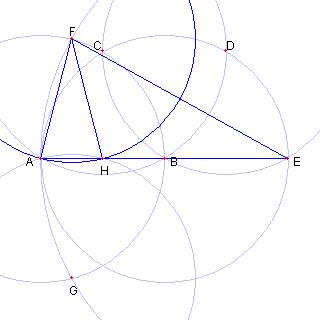
⊿EAF は EA = EF = 2, AF = 1 の 二等辺三角形である。 |
図形の対称性より H は半直線 AE 上にある。 である。 |
|
⊿FHA は二等辺三角形で 低角が同じなので ⊿FAH ∽ ⊿EFA である。よって FA : AH = EF : FA = 2 : 1 また FA = AB = 1 なので AH = 1/2 よって H は AB の中点である |