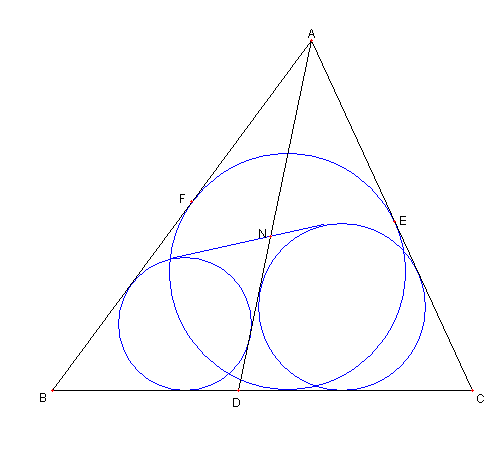
図のように
D は 僊BC の辺 BC 上の点とする
僊BC 内接円と AC, AB との接点を
各々 E, F とする。
僊BD の内接円と 僊DC の内接円の
BC と異なる共通外接戦と AD との交点を
N とする。このとき
AN = AE
である。
解答
|
|
問題 図のように D は 僊BC の辺 BC 上の点とする 僊BC 内接円と AC, AB との接点を 各々 E, F とする。 僊BD の内接円と 僊DC の内接円の BC と異なる共通外接戦と AD との交点を N とする。このとき AN = AE である。 解答 |
|
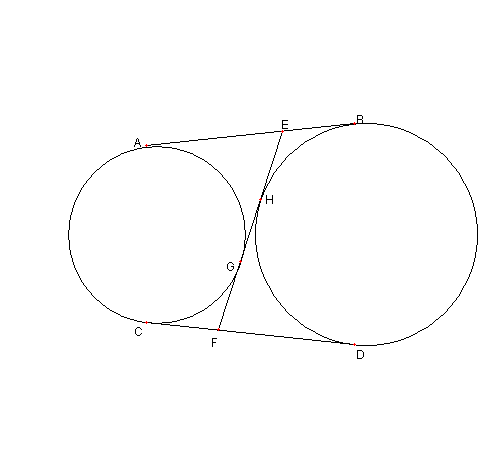
類題 図のように 離れた二円があり AB, CD はその二円の 外接線として E, F は各々 AB, CD 上の点で EF は二円の共通内接線で G, H 各々の接点とする。 |
このとき @ EA = EG = FH = FD A EB = EH = FG = FC B AB = CD = EF EA = EG , FH = FD EB = EH , FG = FC AB = CD はいいでしょう。 残りを示しましょう 解答 |
|
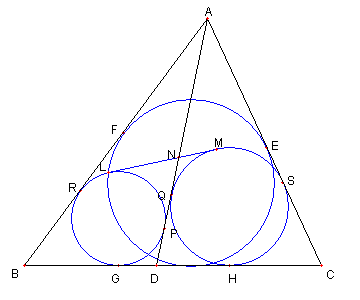
図のように 僊BD の内接円と DB, DA, AB, 共通外接戦との 接点を各々 G, P, R, L とし 僊DC の内接円と DC, DA, AC, 共通外接戦との 接点を各々 H, Q, S, M とする |
このとき、GH = LM より次を得る AP + AQ = AR + AS = AB - BR + AC - CS AB + AC - BG - CH = AB + AC - BC + GH = 2AE + LM 一方 AP + AQ = AN + NP + AN + NQ = 2AN + NL + NM = 2AN + LM よって AE = AN を得る。 Top に戻る |
|
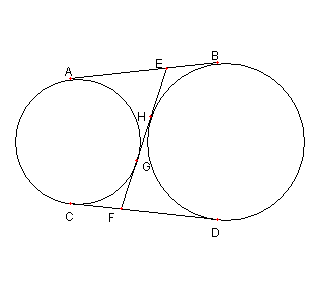
類題の解答 AB = EA + EB = EG + EH = 2EH + HG CD = FC + FD = FG + FH = 2FG + HG AB = CD より EH = FG がわかる。 |
同様に EG = FH がわかる。 AB = EA + EB = EG + EH = FH + EH = EF が示せた。 類題に戻る Top に戻る |