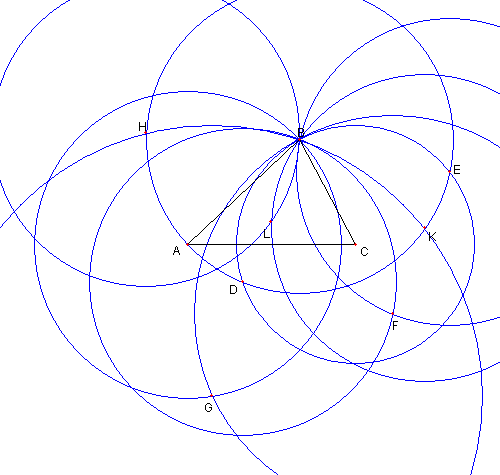
⊿ABC が与えられたとき
左の図はコンパスのみを使って
その外心を作図している図です
以下にその手順に
従って図を書きます
問題はそれで外心の
作図になっていることを示すことです
このサイトでは
2点 A, B が与えられたとき
円 AB で
A を中心とし、半径 AB の円を表します

|
問題 ⊿ABC が与えられたとき 左の図はコンパスのみを使って その外心を作図している図です 以下にその手順に 従って図を書きます 問題はそれで外心の 作図になっていることを示すことです このサイトでは 2点 A, B が与えられたとき 円 AB で A を中心とし、半径 AB の円を表します |
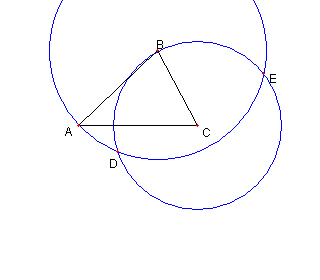
|
|
|
|
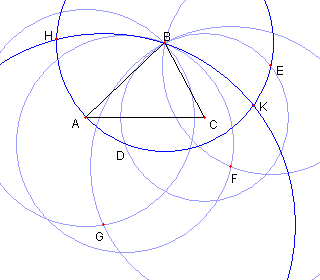
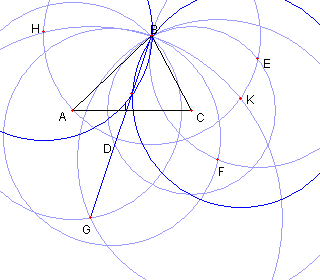
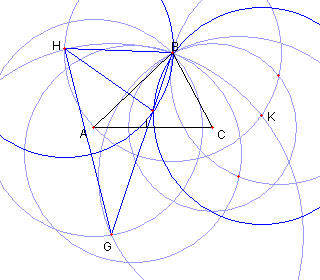
円 BA と円 CB との交点を D と E とおく |
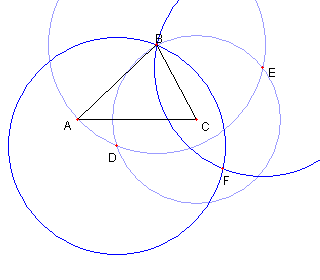
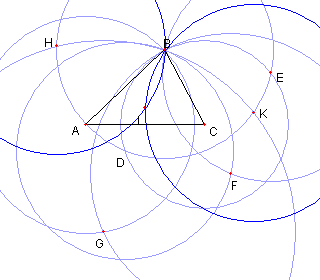
円 DB と円 EB との B と異なる交点を F とおく |
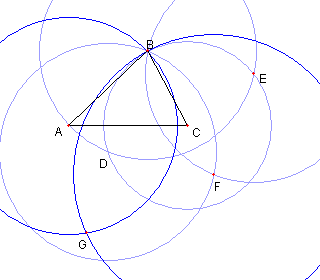
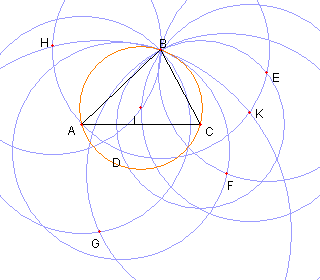
円 FB と円 AB との B と異なる交点を G とおく |
|
|
|
|
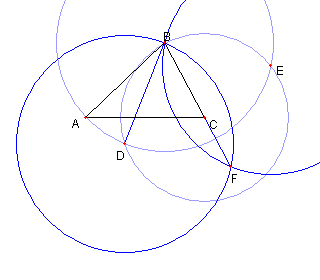
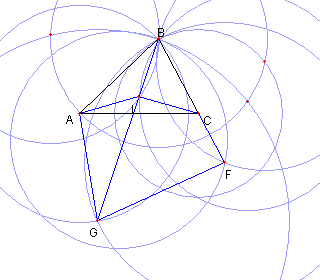
円 GB と円 BA との 交点を H と K とおく |
円 HB と円 KB との B と異なる交点を L とおく |
円 LB を描くと それは ⊿ABC の外接円である |
|
|
|
|
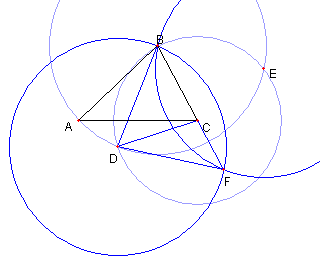
ヒント問題1 F は半直線 BC 上にあり BC×BF = BA2 であることを示せ |
ヒント問題2 G は半直線 BG 上にあり BL×BG = BA2 であることを示せ |
ヒント問題3 (1) BC×BF = BA2 (2) BL×BG = BA2 (3) FB = FG (4) AB = AG を利用して LB = LA = LC を示せ |
|
|
|
|
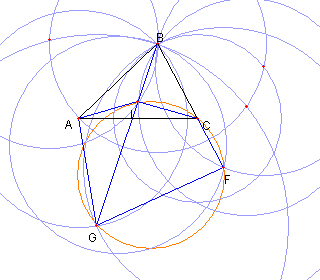
ヒント問題1の解答 D, E が BC に関して対称なので F は半直線 BC 上にある DB = DF, CB = CD に注意しよう CB = CD より ∠BDC = ∠DBC DB = DF より ∠DBC = ∠DFB よって ∠BDC = ∠DFB |
これより BC×BF = BD2 = AB2 |
ヒント問題2の解答 GB = GH, HB = HL より ⊿GHB ∽ ⊿HBL よって BL×BG = BH2 = AB2 |
|
| |
|
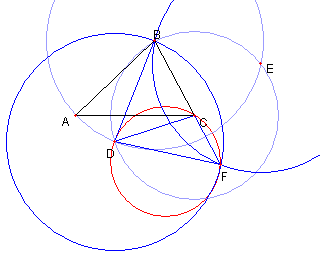
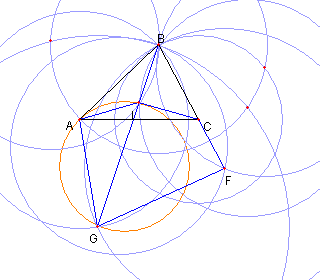
ヒント問題3の解答 (1) BC×BF = BA2 (2) BL×BG = BA2 より BC×BF = BL×BG よって四辺形 LGFC は 円に内接している。 よって、∠BCL = ∠BGF FB = FG より ∠FGB = ∠FBG 故に ∠BCL = ∠CBL よって LB = LC |
(2) BL×BG = BA2 より、BA は ⊿AGL の外接円の 接線である。 よって ∠BAL = ∠AGB AB = AG より ∠AGB = ∠ABG 故に ∠LAB = ∠LBA よって LA = LB 以上より LA = LB = LC |
Top に戻る 手順に戻る ヒント問題に戻る ヒント問題の解答の始めに戻る |