AG の中点を H とする。
KL と OA が直交するようにとる。
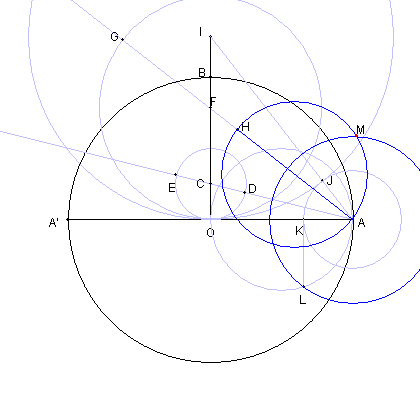
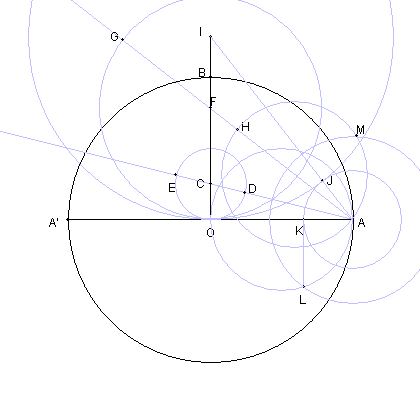
円 AL との交点の一つを M とする。
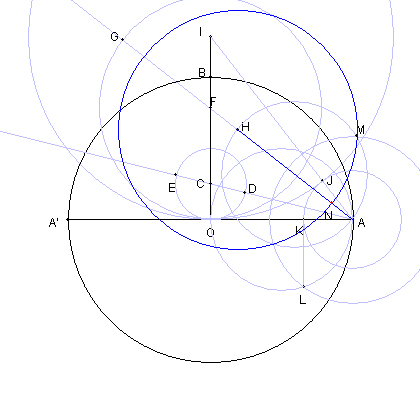
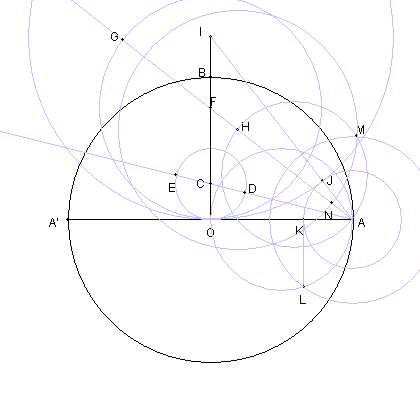
正34角形の一辺の長さである。
 |
 |
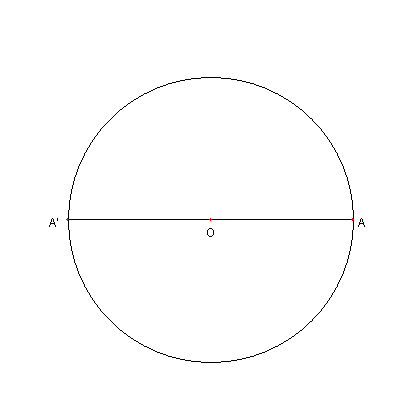
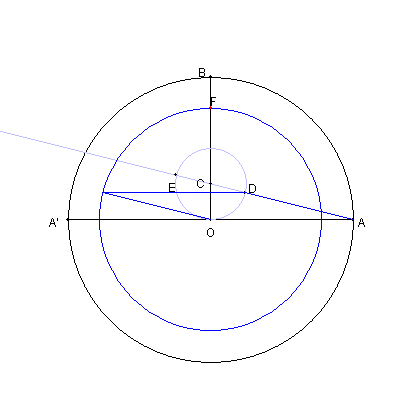
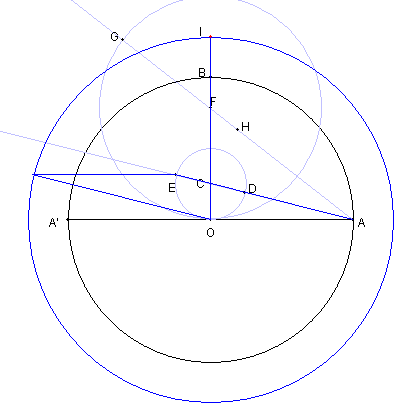
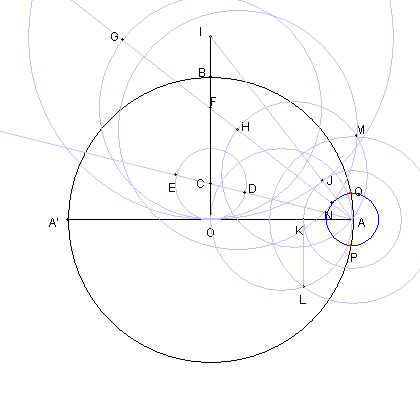
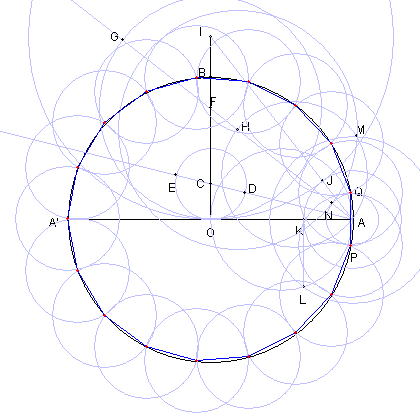
| O を中心とし、AA' を直径とする円をかく。 |
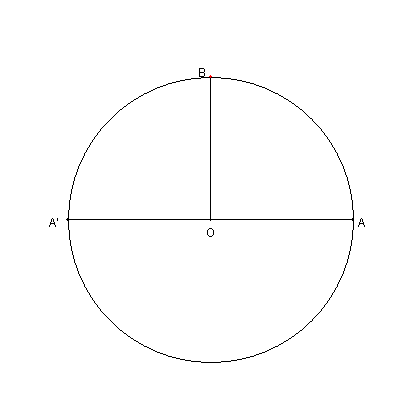
AA' に直交する半径BO をとり |
 |
 |
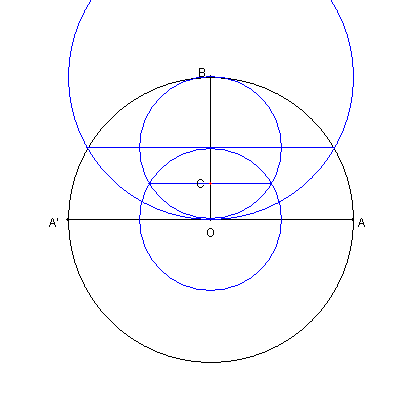
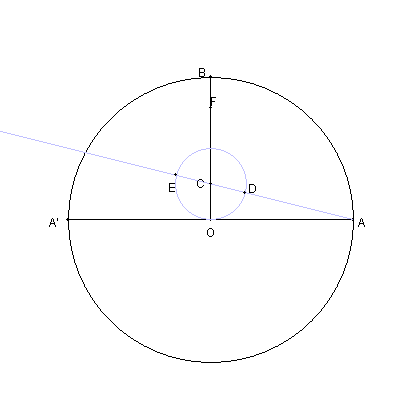
| BO を 3:1 に内分する点を C とおく。 |
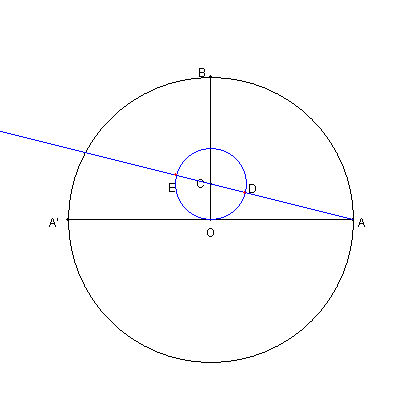
図のように D, E とおく。 |
 |
 |
| OB 上に点 F を OF = AD となるようにとる |
|
 |
 |
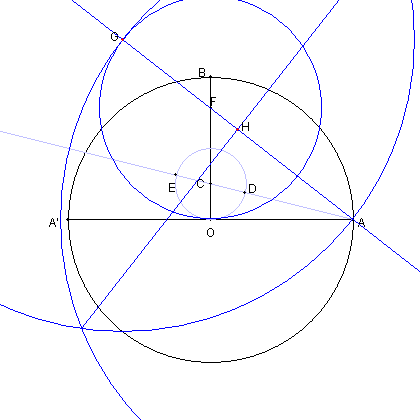
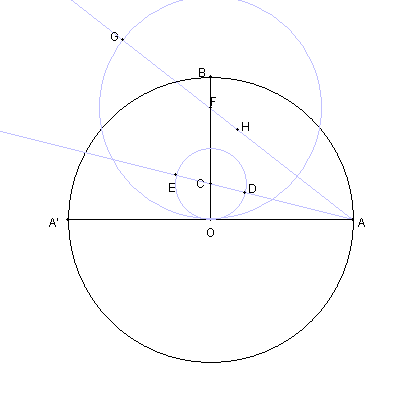
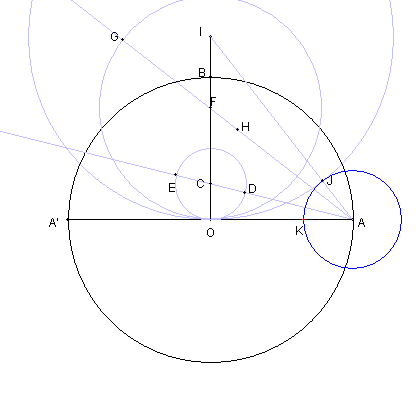
| 円FO と AFの延長との交点を G とおく。 AG の中点を H とする。 |
|
 |
 |
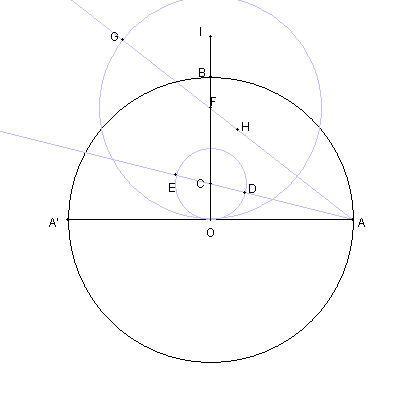
| OB の延長上に点 I を AE = OI となるよにうにとる |
|
 |
 |
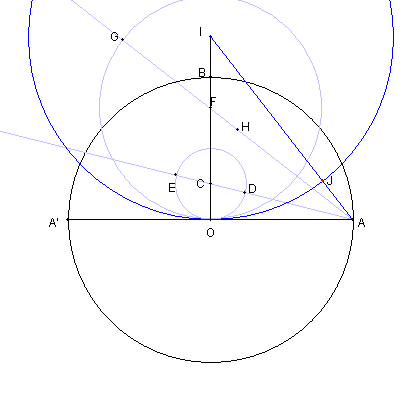
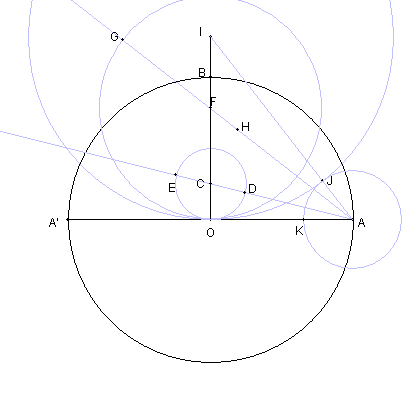
| 円 IO と線分 AI との交点を J とする。 |
|
 |
 |
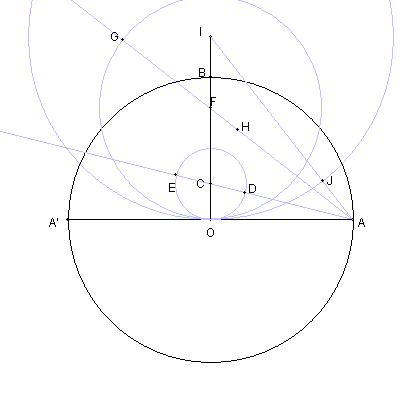
| 円 AJ と 線分 AO との交点を K とする。 |
|
 |
 |
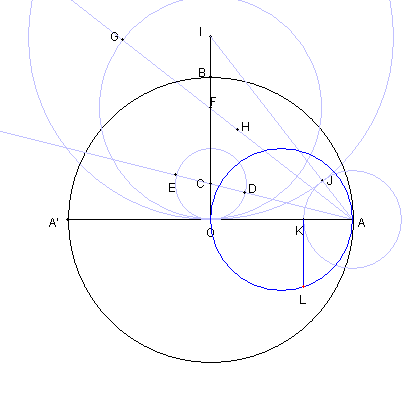
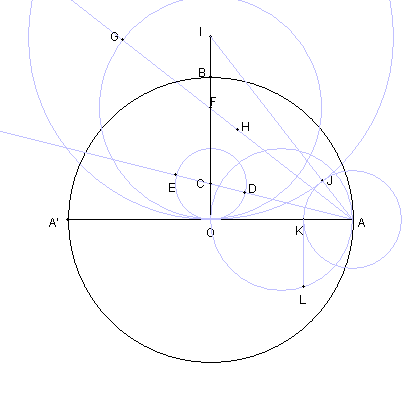
| AO を直径とする円周上に点 L を KL と OA が直交するようにとる。 |
|
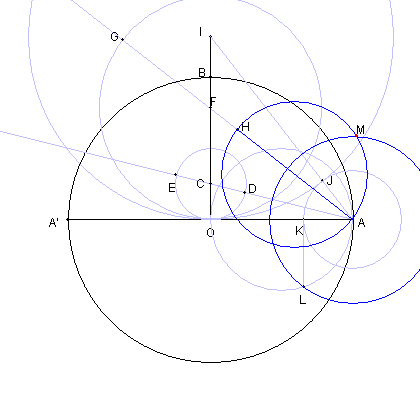 |
 |
| AH を直径とする円と 円 AL との交点の一つを M とする。 |
|
 |
 |
| 円 HM と線分 AH の交点を N とする。 |
|
 |
 |
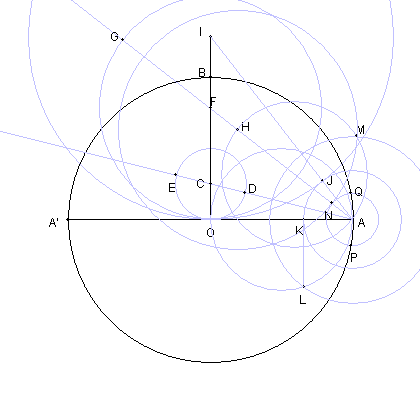
| AN の長さが、円 OA に内接する 正34角形の一辺の長さである。 |
|
 |
 |
 |
|
|
長さが 1 で偏角が 2π/17 の複素数を α で表すと 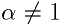 で で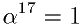 であるので |
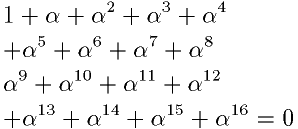
|
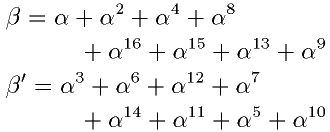 とおくと |
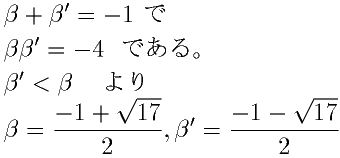 である |
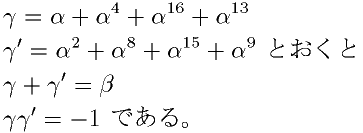 とおくと |
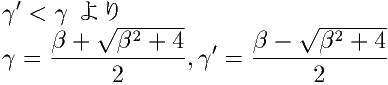 である |
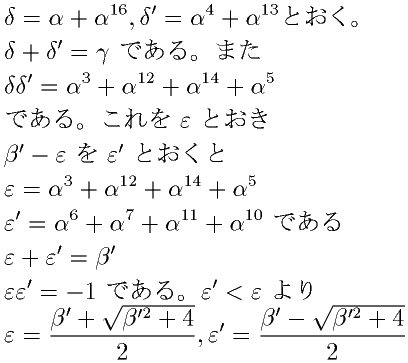
|
 δ' が上記の性質を満たすことの説明は 次を見て下さい |
今までの計算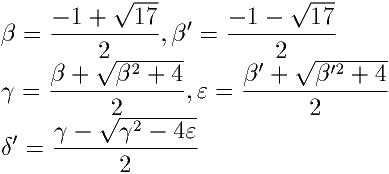 δ' を作図すればよい |

|
 図において、円 O の半径を 1 とする。このとき AD = b, AE = b' である | ||

|
OF = OD = b である | ||

|
参考 
| ||

|
OI = AE = b' である。 | ||

|
参考 
| ||

|
AK = AJ = ε である | ||

|
AO = 1 AK = ε なので AL2 = AK×AO = ε である | ||
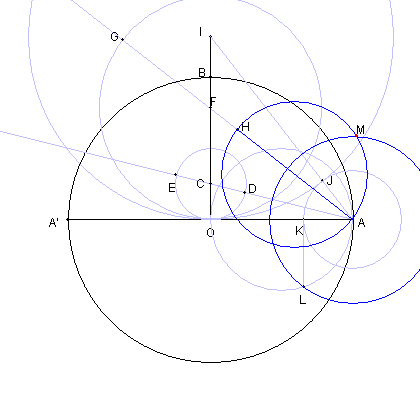
|
| ||

|
参考 
| ||

|
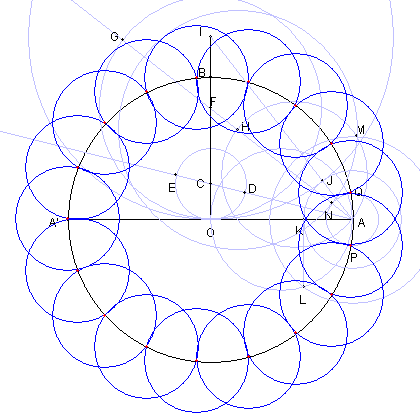
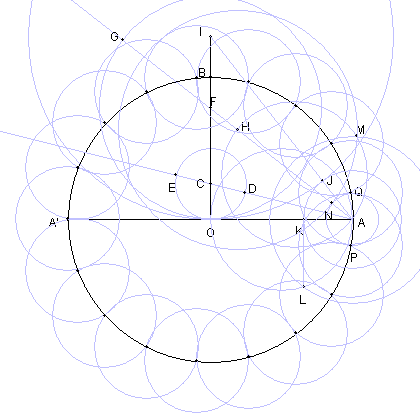
AP = AQ = AN = δ' でこれは、円 O に内接する 正 34 角形の一辺の長さである よって PQ は円 O に内接する 正 17 角形の一辺の長さである 以下の図により 円 O に内接する正 17 角形が作図できる | ||

|

|
|
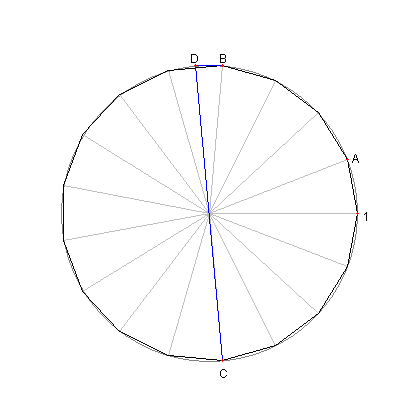
図のように複素数平面で 単位円を 1 から始めて 17 等分する。 点 A に対応する複素数は α 点 B に対応する複素数は α4 点 C に対応する複素数は α13 である。 C の 0 に関する対称点を D とすると 点 D に対応する複素数は -α13 である BD は単位円に内接する正 34 角形の 一辺の長さであり、それは α4 + α13 である。 戻る |