解答2
(1) 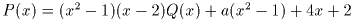 とかける
とかける
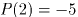 で P(2) = -5 なので、
で P(2) = -5 なので、
余りは 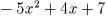 である。
である。
(2) 省略
(4) 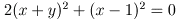 より x = 1, y = -1 である。
より x = 1, y = -1 である。
(5) 方向ベクトル (1,2,a) と (3,1,b) が直交しているので ab = -5 である。
方程式 x = s+1, y = 2s+2, z = as+3, x = 3t-3, y = t-1, z = bt-1 を解く。
x = s+1, y = 2s+2 より y = 2x である。よって
x = 3t-3, y = t-1 なので t-1 = 2(3t-3) であり t = 1 を得る。
t = 1 より x=y=0 を得る。 s=-1 を得る。
z = as+3 = -a+3, z = bt-1 = b-1 より a+b = 4 である。
ab = -5 なので (a,b) = (-1,5) または (a,b) = (5,-1) である。
(a,b)=(-1,5) のとき交点は (0,0,4) であり。
(a,b)=(5,-1) のとき交点は (0,0,2) である。
(6) 略
戻る
メニューに戻る
| 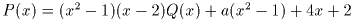 とかける
とかける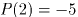 で P(2) = -5 なので、
で P(2) = -5 なので、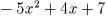 である。
である。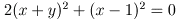 より x = 1, y = -1 である。
より x = 1, y = -1 である。