∠ECB = 15°である。
B から CE の延長に下ろした垂線の足を F
E から BC に下ろした垂線の足を G とする。
BM = 1 とおく。
BF = 2 sin 15°である。
僥BE は直角二等辺三角形なので
BE = 2
sin 15°である。僭EF は 60°、30°の直角三角形なので
BG = (
/2)BE =
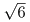sin 15°でEG = (1/2)BR =
sin 15°であるsin 15°= sin(45°- 30°) = (
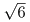-)/4
なのでGM = BM - BG = 1 - (6 - 2
)/4 =
(-1)/2EG = (
-1)/2よって GM = EG なので
∠EMG = 45°である。
よって ∠CEM = 30°である。
これは 漕江君の別解である
一つ戻る