一橋 点 O を中心とする円に四角形 ABCD が内接していて、 次をみたす。 　　AB = 1, BC = CD = 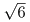, DA = 2 (1)　AC を求めよ。 (2)　v(AO)・v(AD) および v(AO)・v(AC) を求めよ。 (3)　v(AO) = x v(AC) + y v(AD) となる x, y の値を求めよ。 題意の図を描くことを心がけると ∠DAB または ∠ABC を求めればよい。 AC の長さを求めるにも有効という意味で ∠ABC を求めよう θ = ∠ABC とおくと cos ∠ADC = cos (360°- θ) = - cos θ なので AC2 = AB2 + BC2 - 2AB・BC cos θ = 7 - 2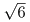cos θ AC2 = DA2 + DC2 + 2DA・DC cos θ = 10 + 4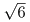cos θ 戻る　　 解答