一橋 点 O を中心とする円に四角形 ABCD が内接していて、 　　AB = 1, BC = CD = 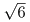, DA = 2　 のとき (1)　AC を求めよ。 (2)　v(AO)・v(AD) および v(AO)・v(AC) を求めよ。 (3)　v(AO) = x v(AC) + y v(AD) となる x, y の値を求めよ。 (1)　θ = ∠ABC とおくと cos ∠ADC = cos (360°- θ) = - cos θ なので AC2 = AB2 + BC2 - 2AB・BC cos θ = 7 - 2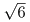cos θ AC2 = DA2 + DC2 + 2DA・DC cos θ = 10 + 4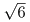cos θ 計算して cos θ -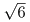/12 で AC = 2 (2)　E, F を AD, AC の中点とすると 　　∠OEA = 90°, ∠OFA = 90°なので 　　v(AO)・v(AD) = AE・AD = 2, v(AO)・v(AC) = AF・AC = 4 (3)　v(CD)・v(CD) = v(AD)・v(AD) + v(AC)・v(AC) - 2 v(AC)・v(AD) より 　　v(AC)・v(AD) = (4 + 8 - 6)/2 = 3 2 = v(AO)・v(AD) = x v(AC)・v(AD) + y v(AD)・v(AD) = 3x + 4y 4 = v(AO)・v(AC) = x v(AC)・v(AC) + y v(AD)・v(AC) = 8x + 3y これを解いて x = 10/23, y = 4/23 戻る　　 解答