問題(京教大00総合)
次の練習問題について考えてみよう。
練習問題 x,y,z > 0 のとき 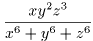 の最大値を求めよ。
の最大値を求めよ。
この練習問題は次の定理(相加相乗平均の定理)を利用すれば簡単に解くことができる。
定理1(相加相乗平均の定理)
n を 2 以上の自然数とする。a1,a2,...,an を
n 個の実数とするとき

が成り立つ。ただし等号は a1 = a2 =... = an
のときのみ成り立つ。
相加相乗平均の定理を用いて、練習問題を解こう。
x,y,x > 0 より相加相乗平均の定理より
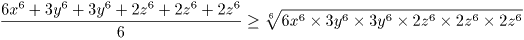
が成り立つ
(等号は 6x6 = 3y6 = 2z6 のときのみ成り立つ)。
これより
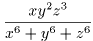

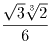
(等号は 6x6 = 3y6 = 2z6 のときのみ成り立つ)。
である。よって、練習問題の答えは 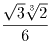 である。
である。
相加相乗平均の定理を利用して次の問題お解きなさい。
問題1 x,y,z > 0 のとき 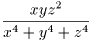 の最大値を求めよ。
の最大値を求めよ。
相加相乗平均の定理は定理1の形よりも、それと同値な次の定理2の形のほうが証明しやすい。
定理2(相加相乗平均の定理)
n を 2 以上の自然数とする。
a1,a2,...,an を
n 個の実数とするとき
a1n + a2n + ... + ann
 na1a2...an
na1a2...an
が成り立つ。ただし等号は a1 = a2 =... = an
のときのみ成り立つ。
定理2の証明には微分を使う方法もあるが、ここでは微分を使わないで数学的帰納法で証明
してみよう。いま次の命題 P(n) を考えることにする。
命題 P(n)
a1,a2,...,an を
n 個の実数とするとき
a1n + a2n + ... + ann
 na1a2...an
na1a2...an
が成り立つ。ただし等号は a1 = a2 =... = an
のときのみ成り立つ。
定理2は 2 以上のすべての自然数 n に対して、命題 P(n) が正しいことを主張している。
定理2の証明1(の概略)
n = 2 のとき、a1,a2 を正の実数とする。このとき
a12 + a22
= 2a1a2 + (a1-a2)2
 2a1a2 より
2a1a2 より
a12 + a22
 2a1a2
(等号は a1 = a2 のときのみ成立する。)
2a1a2
(等号は a1 = a2 のときのみ成立する。)
を得る。つまり P(2) が正しいことがわかる。
次に、 P(4) が正しいことを示そう。
a1,a2,a3,a4 を正の実数とする。このとき
a14 + a24 +
a34 + a44
= (a12)2 + (a22)2 +
(a32)2 + (a42)2
 2(a12a22
+ a32a42)
(P(2)をつかった)
2(a12a22
+ a32a42)
(P(2)をつかった)
 4a1a2a3a4
(P(2)をつかった)
4a1a2a3a4
(P(2)をつかった)
を得る。つまり
a14 + a24 +
a34 + a44
 4a1a2a3a4
4a1a2a3a4
であり、等号は a12 = a22,
a32 = a42,
a1a2 = a3a4 のときのみ成り立つ。
a1,a2,a3,a4 が正であることに注意すると、
等号は a1 = a2 = a3 = a4
のときのみ成り立つことがわかる。つまり P(4) が正しいことがわかる。
次に P(4) が正しいことを利用して P(3) が正しいことを示そう。
a1,a2,a3 を正の実数とする。このとき
b1 = a13/4,
b2 = a23/4,
b3 = a33/4,
b4 =
((a13 + a23 + a33)/3)
1/4 とおくと
b1,b2,b3,b4 は正である。
P(4) を利用して
b14 + b24 +
b34 + b44
 4b1b2b3b4
4b1b2b3b4
を得る。
b14 + b24 +
b34 = 3b44
を利用して、これを変形して
4b44
 4b1b2b3b4
つまり
b44
4b1b2b3b4
つまり
b44
 b1b2b3b4
を得る。これの両辺を 4/3 乗して
b1b2b3b4
を得る。これの両辺を 4/3 乗して
(a13 + a23 + a33)/3
 a1a2a3
a1a2a3
を得る。等号は
b1 = b2 = b3 = b4
のときのみ、つまり
a1 = a2 = a3
のときのみ成り立つ。以上より P(3) が正しいことがわかる。
上と同様な方法を用いて、一般に m を 2 以上の自然数とするとき、
P(2) と P(m) が正しいと仮定して P(2m) が正しいことを示す。
P(2m) が正しいと仮定して P(2m-1) が正しいことを示す。
上の2つを示すことにより、(少し変則的な)数学的帰納法を利用して、定理2が示される。
次の問題に答えよ。
問題2 上記に展開した方法と同様な方法で次を示せ。
(1) P(2) と P(3) が正しいと仮定して P(6) が正しいことを示せ。
(2) P(6) が正しいと仮定して P(5) が正しいことを示せ。
正統的な数学的帰納法を使った定理2の証明を与えよう。
次の定理3を考える。
定理3 n を 2 以上の自然数とする。このとき、正の数 x, y に対して
xn - nxyn-1 + (n-1)yn
 0
(等号は x = y のときのみ成り立つ)
0
(等号は x = y のときのみ成り立つ)
定理3は次の補題1を使って証明することができる。
補題1 n を 2 以上の自然数とする。このとき、
xn - nxyn-1 + (n-1)yn
= (x-y)2(xn-2 + 2xn-3y +
3xn-4y2 + ... + (n-1)yn-2)
が成り立つ。
定理3は次の補題2を使っても証明することができる。
補題2 n を 2 以上の自然数として、
fn(x) = xn - nx + (n-1) とおく。
このとき、次が成り立つ。
(1) x > 0 のとき fn(x)  0 である。
(等号は x = 1 の時のみ成り立つ。)
0 である。
(等号は x = 1 の時のみ成り立つ。)
(2) x, y > 0 のとき fn(x/y)yn  0 である。
(等号は x = y の時のみ成り立つ。)
0 である。
(等号は x = y の時のみ成り立つ。)
問題3 補題2の(1)を fn(x) の増減を調べることにより証明せよ。
定理3を利用すると定理2を証明することができる。例として P(2) が正しいと仮定して
P(3) が正しいことを示してみよう。
a1,a2,a3 を正の実数とする。このとき定理3より
a33 + 2a13
 3a3a12
3a3a12
a33 + 2a23
 3a3a22
3a3a22
を得る。これより
2(a13 + a23 + a33)
 3a3(a12 + a22) が成り立つ
(等号は a1 = a2 = a3
のときのみ成り立つ)。
3a3(a12 + a22) が成り立つ
(等号は a1 = a2 = a3
のときのみ成り立つ)。
P(2) より a12 + a22
 2 a1a2 である(等号は a1 = a2
のときのみ成り立つ。)から
2 a1a2 である(等号は a1 = a2
のときのみ成り立つ。)から
a13 + a23 + a33
 3a1a2a3 が成り立つ。
3a1a2a3 が成り立つ。
等号は
a1 = a2 = a3
のときのみ成り立つ。
上の例と同様な方法で m が 2 以上の整数のとき、P(m) が成り立つと仮定して
P(m+1) が成り立つことが示される。つまり定理2が証明できる。
問題4
上の例と同様な方法で m が 2 以上の整数のとき、P(m) が成り立つと仮定して
P(m+1) が成り立つことを示せ。
解答
戻る
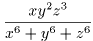 の最大値を求めよ。
の最大値を求めよ。
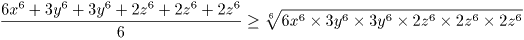
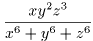

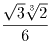
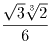 である。
である。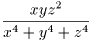 の最大値を求めよ。
の最大値を求めよ。 na1a2...an
na1a2...an na1a2...an
na1a2...an 2a1a2 より
2a1a2 より 2a1a2
(等号は a1 = a2 のときのみ成立する。)
2a1a2
(等号は a1 = a2 のときのみ成立する。) 2(a12a22
+ a32a42)
(P(2)をつかった)
2(a12a22
+ a32a42)
(P(2)をつかった) 4a1a2a3a4
(P(2)をつかった)
4a1a2a3a4
(P(2)をつかった) 4a1a2a3a4
4a1a2a3a4 4b1b2b3b4
4b1b2b3b4 4b1b2b3b4
つまり
b44
4b1b2b3b4
つまり
b44
 b1b2b3b4
を得る。これの両辺を 4/3 乗して
b1b2b3b4
を得る。これの両辺を 4/3 乗して a1a2a3
a1a2a3 0
(等号は x = y のときのみ成り立つ)
0
(等号は x = y のときのみ成り立つ) 0 である。
(等号は x = 1 の時のみ成り立つ。)
0 である。
(等号は x = 1 の時のみ成り立つ。) 0 である。
(等号は x = y の時のみ成り立つ。)
0 である。
(等号は x = y の時のみ成り立つ。) 3a3a12
3a3a12 3a3a22
3a3a22 3a3(a12 + a22) が成り立つ
(等号は a1 = a2 = a3
のときのみ成り立つ)。
3a3(a12 + a22) が成り立つ
(等号は a1 = a2 = a3
のときのみ成り立つ)。 2 a1a2 である(等号は a1 = a2
のときのみ成り立つ。)から
2 a1a2 である(等号は a1 = a2
のときのみ成り立つ。)から 3a1a2a3 が成り立つ。
3a1a2a3 が成り立つ。