問題
問題1 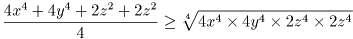 より最大値は
より最大値は 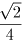 である。
である。
問題2 (1)
a1,a2,
a3,a4,
a5,a6 を正の実数
とする。このとき
P(2) より
a16 + a26
 2a13a23
2a13a23
a36 + a46
 2a33a43
2a33a43
a56 + a66
 2a53a63
2a53a63
が成り立つ。また P(3) より
a13a23 +
a33a43 +
a53a63
 3a1a2a3a4a5a6
が成り立つ。したがって
3a1a2a3a4a5a6
が成り立つ。したがって
a16 + a26 +
a36 + a46 +
a56 + a66
 6a1a2a3a4a5a6
が成り立つ。
6a1a2a3a4a5a6
が成り立つ。
等号が成り立つのは
a16 = a26,
a36 = a46,
a56 = a66,
a13a23 =
a33a43 =
a53a63
の時のみである。
a1,a2,
a3,a4,
a5,a6 は正なので、
等号が成り立つのは
a1 = a2 =
a3 = a4 =
a5 = a6 のときのみである。
よって P(6) が示せた。
(2) a1,a2,
a3,a4,
a5 を正の実数
とする。いま
b1 = a15/6,
b2 = a25/6,
b3 = a35/6,
b4 = a45/6,
b5 = a55/6,
b6 =
((a15 + a25
+ a35 + a45
+ a55)/5)1/6 とおくと
b1,b2,b3,b4
,b5,b6は正である。
ここで
b16 = a15,
b26 = a25,
b36 = a35,
b46 = a45,
b56 = a55 であり
b16 + b26 +
b36 + b46 +
b56 = 5b66
である。
P(6) より
b16 + b26 +
b36 + b46 +
b56 + b66
 6b1b2b3b4b5b6
である。これより
6b1b2b3b4b5b6
である。これより
6b66
 6b1b2b3b4b5b6
つまり
b65
6b1b2b3b4b5b6
つまり
b65
 b1b2b3b4b5
を得る。
したがって、両辺を 6/5 乗し 5 倍して
b1b2b3b4b5
を得る。
したがって、両辺を 6/5 乗し 5 倍して
a15 + a25 +
a35 + a45 +
a55
 5a1a2a3a4a5
を得る。
5a1a2a3a4a5
を得る。
等号は
b1 = b2 =
b3 = b4 =
b5 = b6 のときのみ、つまり、
a1 = a2 =
a3 = a4 =
a5 のときのみである。
問題3 fn'(x) = n(xn-1 - 1)
であり fn(1) = 0, fn'(1) = 0 である。
後は略
問題4
a1,a2,...,am+1 を正の実数とする。このとき定理3より
am+1m+1 + ma1m+1
 (m+1)am+1a1m
(m+1)am+1a1m
am+1m+1 + ma2m+1
 (m+1)am+1a2m
(m+1)am+1a2m
.
.
am+1m+1 + mamm+1
 (m+1)am+1amm
(m+1)am+1amm
を得る。これより
m(a1m+1 + a2m+1 +
... + am+1m+1)
 (m+1)am+1(a1m
+ a2m + ... + amm) が成り立つ
(等号は a1 = a2 = ... = am+1
のときのみ成り立つ)。
(m+1)am+1(a1m
+ a2m + ... + amm) が成り立つ
(等号は a1 = a2 = ... = am+1
のときのみ成り立つ)。
P(m) より a1m + a2m
+ ... + amm
 m a1a2...am である
(等号は a1 = a2 = ... = am
のときのみ成り立つ。)から
m a1a2...am である
(等号は a1 = a2 = ... = am
のときのみ成り立つ。)から
a1m+1 + a2m+1
+ ... + am+1m+1
 (m+1)a1a2...am+1 が成り立つ。
(m+1)a1a2...am+1 が成り立つ。
等号は
a1 = a2 = ... = am+1
のときのみ成り立つ。
戻る
メニューに戻る
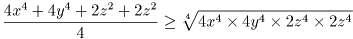 より最大値は
より最大値は 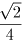 である。
である。 2a13a23
2a13a23 2a33a43
2a33a43 2a53a63
2a53a63 3a1a2a3a4a5a6
が成り立つ。したがって
3a1a2a3a4a5a6
が成り立つ。したがって 6a1a2a3a4a5a6
が成り立つ。
6a1a2a3a4a5a6
が成り立つ。 6b1b2b3b4b5b6
である。これより
6b1b2b3b4b5b6
である。これより 6b1b2b3b4b5b6
つまり
b65
6b1b2b3b4b5b6
つまり
b65
 b1b2b3b4b5
を得る。
したがって、両辺を 6/5 乗し 5 倍して
b1b2b3b4b5
を得る。
したがって、両辺を 6/5 乗し 5 倍して 5a1a2a3a4a5
を得る。
5a1a2a3a4a5
を得る。 (m+1)am+1a1m
(m+1)am+1a1m (m+1)am+1a2m
(m+1)am+1a2m (m+1)am+1amm
(m+1)am+1amm (m+1)am+1(a1m
+ a2m + ... + amm) が成り立つ
(等号は a1 = a2 = ... = am+1
のときのみ成り立つ)。
(m+1)am+1(a1m
+ a2m + ... + amm) が成り立つ
(等号は a1 = a2 = ... = am+1
のときのみ成り立つ)。 m a1a2...am である
(等号は a1 = a2 = ... = am
のときのみ成り立つ。)から
m a1a2...am である
(等号は a1 = a2 = ... = am
のときのみ成り立つ。)から (m+1)a1a2...am+1 が成り立つ。
(m+1)a1a2...am+1 が成り立つ。