(1) f'(x) = (1+x/
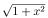 /(x+
/(x+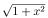 )
= 1/
)
= 1/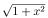 である。
である。(2) 曲線は媒介変数表示で
x = θ cos(θ), y = θ sin(θ) と表される。
dx/dθ = cos(θ) - θ sin(θ), dy/dθ = sin(θ) + θ cos(θ) である。
(dx/dθ)2 + (dy/dθ)2 = 1 + θ2 であるので
求める曲線の長さは
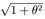 を θ に関して 0 から
π まで積分したものである。
を θ に関して 0 から
π まで積分したものである。それは θ の代わりに x を使うと
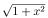 を x に関して 0 から
π まで積分したものである。
を x に関して 0 から
π まで積分したものである。d(x
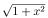 )/dx =
)/dx =
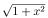 + x2/
+ x2/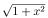
=
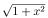 + (1+x2-1)/
+ (1+x2-1)/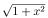
= 2
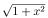 - 1/
- 1/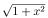 であるから
であるから(1) の結果とあわせると
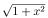 の原始関数は
の原始関数は(x
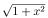 + log(x+
+ log(x+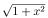 ))/2
であることがわかる。
))/2
であることがわかる。よって求める長さは (π
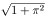 ) +
log(π+
) +
log(π+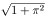 )/2 である。
)/2 である。戻る