１ 数列 {an} の初項 a1 から第 n 項 an までの和を Sn と表す。この数列が
a1 = 1, Sn
1 (n ∞ のとき)、
n(n-2) an+1 = Sn (n ≥ 1)を満たすとき、一般項 an を求めよ。
２ 半径１の円周上に相ことなる３点 A, B, C がある。
(1) AB2+BC2+CA2 > 8 ならば 僊BC は鋭角三角形であることを示せ。
(2) AB2+BC2+CA2 ≤ 9 が成立することを示せ。 また、等号が成立するのはどのような場合か。
３ f(x) = x4 + ax3 + bx2 + cx + 1 は 整数を係数とする x の 4 次式とする。４次方程式 f(x) = 0 の重複を含めた４つの 解のうち、２つは整数で残り２つは虚数であるという。 このとき a,b,c の値をもとめよ。
４ (1) x ≥ 0 で定義された関数 f(x) = log(x+
)
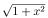について導関数 f'(x) をもとめよ。(2) 極方程式 r = θ (θ ≥ 0) で定義された曲線の 0 ≤ θ ≤ π の部分の長さを求めよ。
５ a,b,c を実数とする。y = x3 + 3ax2 + 3bx と y = c のグラフが相異なる３つの交点を持つという。
このとき a2 > b が成立することを示し、これらの交点の x 座標は すべて
開区間 (-a - 2root(a2 - b),-a + 2root(a2 - b)) に含まれることを示せ。
６ 0 < θ < 90 とし a は正の数とする。複素数平面上の点 z0, z1, z2, ... を 次の条件 (i)(ii) を満たすように定める。
(i) z0 = 0, z1 = a
(ii) n ≥ 1 のとき 点 zn - zn-1 を原点のまわりに θ°回転すると zn+1 - zn と一致する。
このとき点 zn (n ≥ 1) が点 z0 と一致するような n が存在する必要十分条件は θ が有理数であることを示せ。
| １の解答 | ２の解答 | ３の解答 |
| ４の解答 | ５の解答 | ６の解答 |