4 行列 A, B を A =  ,
B =
,
B = 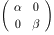 とする。
とする。
次の (*) が成り立つための実数 α β についての必要十分条件
をもとめよ。
(*) どんな2次正方行列 Y に対しても2次正方行列 X で
AX - XB = Y となるものがある。
解答
(*) を成分で表現すると次の (**) と同値である。
(**) x,y,z,w を未知数とする連立一次方程式
(2-&alpha)x = p
(2-β)y = q
x + (1-α)z = r
y + (1-β)w = s
がすべての数の組 (p,q,r,s) に対して解をもつ。
いま (*) が成り立ったとする。つまり (**) が成り立ったとする。このとき
(p,q,r,s) = (1,0,0,0) のときも (**)の方程式が解をもつので α ≠ 2
(p,q,r,s) = (0,0,1,0) のときも (**)の方程式が解をもつので α ≠ 1
(なぜなら α = 1 と仮定する。このとき解(x,y,z,w) があると (2-α)x = p = 0 より x = 0,
x + (1-α)z = r より 0 = r = 1 となり矛盾)
(p,q,r,s) = (0,1,0,0) のときも (**)の方程式が解をもつので β ≠ 2
(p,q,r,s) = (0,0,0,1) のときも (**)の方程式が解をもつので β ≠ 1
以上より α ≠ 2 かつ α ≠ 1 がつ β ≠ 2 かつ β ≠ 1 となる。
逆に α ≠ 2 かつ α ≠ 1 がつ β ≠ 2 かつ β ≠ 1 とすると
任意の数の組 (p,q,r,s) に対して (**) における連立一次方程式は
x = p/(2-α)、y = q/(2-β), z = (r - p/(2-α))/(1-α),
w = (s - q/(2-β))/(1-β)
と解ける。つまり (**) が成立し、従って (*) も成立する。
以上より
(*) が成立するための α β についての必要十分条件は
α ≠ 2 かつ α ≠ 1 がつ β ≠ 2 かつ β ≠ 1 である。
戻る
 ,
B =
,
B = 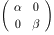 とする。
とする。