京大(04前理) １　f(θ) = cos 4θ - 4 sin2 θ とする。 0 ≤ θ ≤ (3π)/4 における f(θ) の最大値と最小値を求めよ ２　α > 0 とし x > 0 で定義された関数 　　f(x) = (e/xα - 1)×(log x)/x を考える。 y = f(x) のグラフより下側で x 軸より上側の部分の面積を α で表せ。 ただし e は自然対数の底である。 ３　n を 2 以上の自然数とする。 x2n を x2 - x + (n-1)/n2 で割ったあまりを anx + bn とする。 即ち x の多項式 Pn(x) があって 　　x2n = (x2 - x + (n-1)/n2)Pn(x) + anx + bn が成り立っているとする。 n ∞ のときの an と bn の極限値を 求めよ。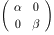(表現を少し変えてあります) ４　行列 A, B を A = , B = とする。 次の (*) が成り立つための実数 α β についての必要十分条件 をもとめよ。 (*)　どんな２次正方行列 Y に対しても２次正方行列 X で 　 　　AX - XB = Y となるものがある。 ５　　複素数 α に対して その共役複素数を α で表す。 α を実数でない複素数とする。 複素平面内の円 C が 1, -1, α を通るならば C は -1/α も通ることを示せ。 ６ N を自然数とする N+1 個の箱があり 1　から N+1 までの番号が付いている。どの箱 にも玉が１個入っている。１から N までの箱に入っている玉は白玉で番号 N+1 の箱に入っている玉は赤玉である。次の操作 (*) を各々の k = 1, 2, ..., N にたいしして k が小さい ほうから順番に１回ずつ行う。 (*)　k 以外の番号の N 個の箱から１個箱をその選び、その箱の中身と番号の k 箱の中身を交換する （ただし、個の箱から１個の箱を選ぶ事象は、どれも同様に確からしいとする） 操作がすべて終了したのちに、赤玉が番号 N+1 の箱に入っている確率を求めよ。 　１の解答 　２の解答 　３の解答 　４の解答 　５の解答 　６の解答