２　x, y を相異なる正の実数とする。数列 {an} を 　　　　a1 = 0, an+1 = xan + yn+1 (n = 1, 2, 3, ...) 　　　によって定めるとき、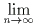an が有限の値に収束するような 　　座標平面上の点 (x,y) の範囲を図示せよ。 x ≠ 0 に注目しておく bn = an/xn, z = y/x とおくと 　　　　b1 = 0, bn+1 = bn + zn+1 である。z ≠ 1 に注目しておく。 n ≥ 2 のときは 　　　　bn = z2 + z3 + ... + zn 　　　　　　　　= z2(1-zn-1) /(1-z)　 よって 　　　　an = y2(xn-1-yn-1) /(x-y) 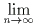an が有限の値に収束するので 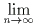(an+1 - xan) も有限の値に収束する つまり 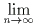yn+1 も有限の値に収束する 0 < y だったので 0 < y ≤ 1 である。 　　　　an = y2(xn-1-yn-1) /(x-y) で 0 < y < 1 で 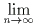an が有限の値に収束するので 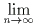xn-1 も有限の値に収束する 0 < x だったので 0 < x ≤ 1 である。 逆に、 0 < x ≤ 1 、 0 < y ≤ 1 、y ≠ x のときには 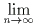an は有限の値に収束する。 もとめる、図形は左図のとおりである。 x = 0, y = 0, y=x は取り除く 　戻る