１ (1) 定積分
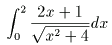を求めよ(2) 一歩で一段または二段のいづれかで階段を昇るとき、
一歩で二段を昇ることは連続しないものとする。
１５段の階段を昇る昇り方は何通りか。
２ x, y を相異なる正の実数とする。数列 {an} を
a1 = 0, an+1 = xan + yn+1 (n = 1, 2, 3, ...)
によって定めるとき、
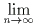an が有限の値に収束するような座標平面上の点 (x,y) の範囲を図示せよ。
３ p を 3 以上の素数とする。
4 個の整数 a, b, c, d が次の 3 条件
a + b + c + d = 0, ad - bc + p = 0, a ≥ b ≥ c ≥ d
を満たすとき、 a, b, c, d を p を用いて表せ。
４ 点 O を中心とする円の円に内接する 僊BC の
３辺 AB, BC, CA をそれぞれ 2 : 3 に内分する点を
P, Q, R とする。
儕QR の外心が O と一致するとき、
僊BC はどのような三角形か。
５ A を２次の正方行列とする。 列ベクトル
0 に対し列ベクトル
1, 2, 3 .... をn+1 = An (n = 0, 1, 2, ....)ある零ベクトルでない
0 について 3 以上の自然数 m で初めてm が 0 と一致するとき、行列 Am は単位行列であることを示せ。６ すべての実数で定義され何回でも微分できる関数 f(x) が
f(0) = 0, f'(0) = 1 を満たし
さらに、任意の実数 a, b に対し 1 + f(a)f(b) ≠ 0 であって
f(a+b) = (f(a)+f(b))/(1 + f(a)f(b))
を満たしている
(1) 任意の実数 a に対して -1 < f(a) < 1 であることを証明せよ。
(2) y = f(x) のグラフは x > 0 で上に凸であることを示せ。
| １の解答 | ２の解答 | ３の解答 |
| ４の解答 | ５の解答 | ６の解答 |