2004年度採用試験(京都府高校)

１．次の各問いに答えなさい。ただし、解答欄には答えのみ書きなさい。
(1) 　

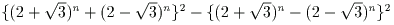
　　　　　を簡単にしなさい。
(2)　n を 2 以上の整数とするとき, xⁿ を x²-1 で割った余りを求めなさい。
(3)　n 個のさいころを振って、出た目の積が 5 の倍数となる確率を求めなさい。

(4)　xy 平面上の２定点を A(1,-1), B(2,3) とし、動点 P が y 軸上を動くとき、AP + PB が
　　　最小となる点 P の座標を求めなさい。

解答
(1)　4
(2)　n が偶数のとき 1, n が奇数のとき x
　　　　((1-(-1)ⁿ)/2)x + (1+(-1)ⁿ)/2 　　　でもよい
(3)　1 - (5/6)ⁿ
(4)　(0, 1/3)

解説
(1)　(a + 1/a)² - (a - 1/a)² の形
(2)　x^m - 1 = (x-1)(x^m-1 + x^m-2 + ... + x + 1) より
　　　x^2m - 1 = (x²-1)(x^2m-2 + x^2m-4 + ... + x² + 1)
　　　x^2m+1 - x = (x²-1)(x^2m-2 + x^2m-4 + ... + x² + 1)x
(3)　5 が一回でもでる確率なので 1 - (5 が一度も出ない確率) が求めるもの。
(4)　y 軸に関して B と対称な点 C(-2,3) をとり AC と y 軸との交点が求める点である。

戻る　　　 indexに戻る