(1)
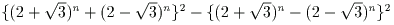
を簡単にしなさい。
(2) n を 2 以上の整数とするとき, xn を x2-1 で割った余りを求めなさい。
(3) n 個のさいころを振って、出た目の積が 5 の倍数となる確率を求めなさい。
(4) xy 平面上の２定点を A(1,-1), B(2,3) とし、動点 P が y 軸上を動くとき、AP + PB が
最小となる点 P の座標を求めなさい。
２． 次の各問いに答えなさい。ただし、(1) については答えのみでよい。
(1) あるクラスで、「１，２，３ の３つの数字を1つずつ用いて、なるべく大きな整数を表しなさい。」 という問題を
出題したところ、次の５通りの解答を得た。これらを小さい順に左から不等号を用いて並べなさい。
321, 312, 213, 321, 231
(2) ２，３，４ の３つの数字を1つずつ用いて、なるべく大きな整数を表しなさい。
また、その整数は何桁になるか。ただし log102 = 0.3010, log103 = 0.4771 として計算しなさい。
３． 平面上に高さが異なる３つの塔がそれぞれ平面と垂直に立っている。P さんが、平面上の 異なる３地点 A, B, C から、これらの塔の先端を眺めたところ、A, B, C のどの地点でも、３つの塔のうち の２つの塔の先端が重なって見えた。このとき、３地点 A, B, C が一直線上にあることを証明しなさい。
∞ のときの an の極限が 2 であることを示せ。
(表現が変えてあります)