|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
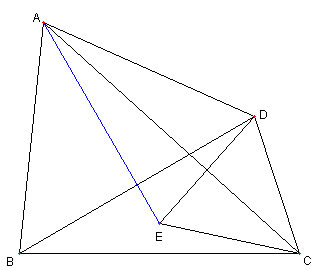
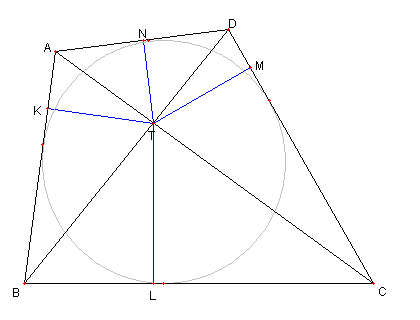
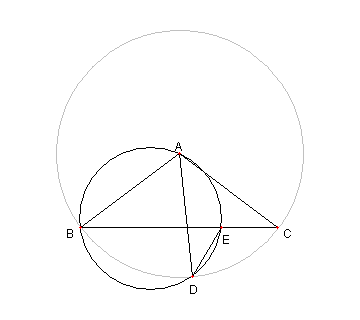
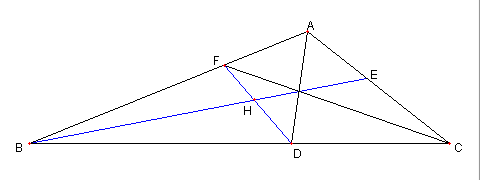
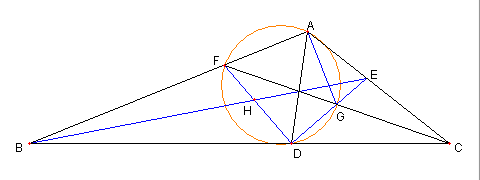
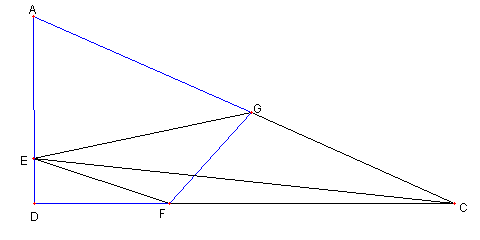
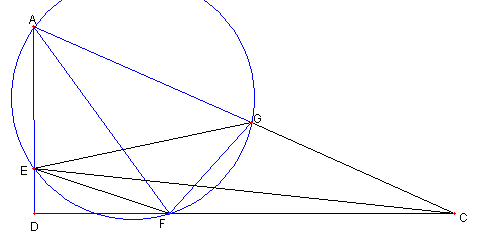
二つの正三角形と内接円と傍接円
図において
⊿ABC は正三角形
D は AC の中点で、E は AD の中点
⊿BFE は正三角で
G は BD の中点で,
H は BC と GF との交点とする
このとき
G が ⊿ABH の内接円の中心(内心)
F が ⊿AHC の傍接円の中心(傍心)で
この二つの円の大きさが同じ
であることを示せ
解説 Applet版
|
|
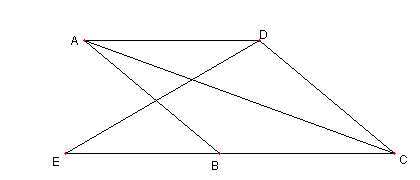
40°の菱形と対角線
図において
四辺形 ABCD は菱形で ∠BAD = 40°とする
CB の延長上に点 E を
CE = CA
とする
このとき
∠DEC = 30°
であることを示せ
解説 Applet版
|
|
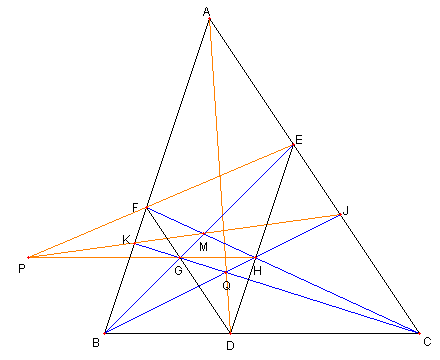
三角形と一点で会する3直線
D, E, F を各々 ⊿ABC の
辺 BC, CA, AB 上の点で
DE ∥ AB, DF ∥ AC とする。
G を BE と DF の交点とし、
H を DE と CF の交点とする
J を BH と AC の交点とし、
K を CG と AB の交点とする
このとき次を示せ。
(1) GH は BC と平行である。
(2) AD, BJ, CK は一点で交わる
(3) BE, CF, JK は一点で交わる
(4) EF, GH, JK は一点で交わる
Go Geometryにあった問題です
解説 Applet版
|
|
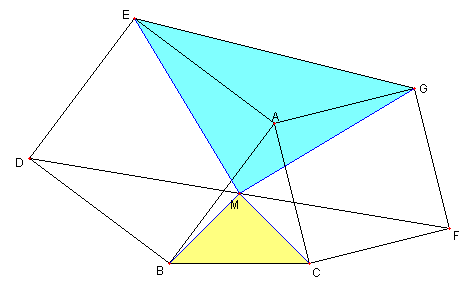
二つの正方形と二つの直角二等辺三角形
図において
四辺形 ABDE と ACFG は正方形とする。
M を DF の中点とするとき
⊿MBC, ⊿BEG は直角二等辺三角形である。
このことを示せ。
解説 Applet版
|
|
30°問題
図において
∠ABC = 84°、∠ACB = 42°
∠DBC = 30°、∠ACD = 30°
⊿CDE は正三角形とする。
このとき AE が BD を垂直二等分する
ことを示せ。
解説 Applet版
|
|
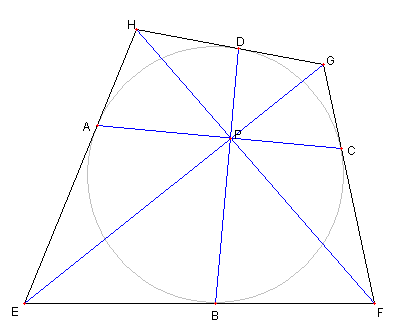
円に外接する四辺形と直交する弦
四辺形 EFGH は円に外接しているとする。
その円と、辺 HE, EF, FG, GH 各々との接点を
A, B, C, D とする
4直線 EG, FH, AC, BD が一点で交わっている
(参照)
その交点を P とする。
AC と BD が直交しているとき
次が成り立つことを示せ。
PB は ∠EPF の二等分線である
解説 Applet版
|
|
|
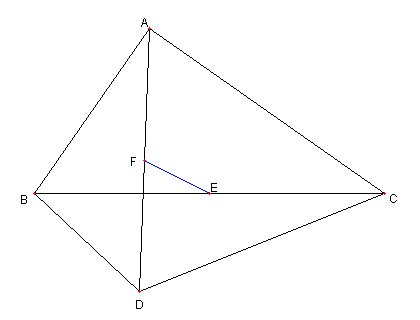
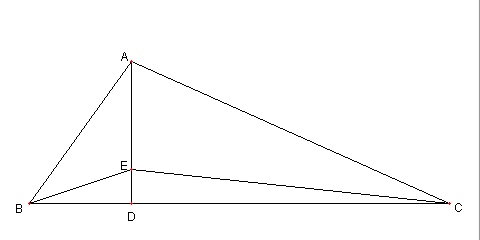
直角三角形と二等辺三角形と中点
⊿ABC は ∠BAC = 90°の直角三角形
⊿ADC は DA = DC の二等辺三角形
E は BC の中点とし、
F は AD の中点とする
このとき、次を示せ。
BD = 2EF である
解説 Applet版
|
|
|
円に外接する四辺形と長さ
四辺形 ABCD は円に外接しているとする。
T を対角線 AC と BD との交点とする。
T から辺 AB, BC, CD, DA 各々に
下ろした垂線の足を各々 K, L, M, N とおく
h1 = TK,
h2 = TL,
h3 = TM,
h4 = TN
とおくとき、次が成り立つことを示せ。
1/ h1 + 1/h3 =
1/ h2 + 1/h4
解説 Applet版
|
|
|
角度の問題(36°)
図において
D は ⊿ABC の頂点 A から
辺 BC に下ろした垂線の足とする。
∠BAD = 36°, ∠CAD = 66°とする
E は AD 上の点で
∠ACE = 18°とする。このとき
∠EBC = 18°であることを示せ。
解説 Applet版
角度の問題(38°)の発展問題
|
|
|
角度の問題(38°)
図において
AB = AD で ∠ABD = 14°
∠CBD = 16°, ∠CDB = 8°
とするとき
∠BAC = 38°であることを示せ。
(かなりの難問と思います)
解説 Applet版
|
|
|
60°の三角形と垂心
⊿ABC において ∠ABC = 60°とする。
H は ⊿ABC の垂心
D, E, F は ⊿ABC の頂点 A, B, C から
各々辺 BC, CA, AB に引いた垂線の足とし
M は BH の中点とする。
CM の延長線上に点 G を
GM = MC となるようにとる。
K を AG の中点とするとき次を示せ。
⊿KBH は正三角である。
解説 Applet版
|
|
|
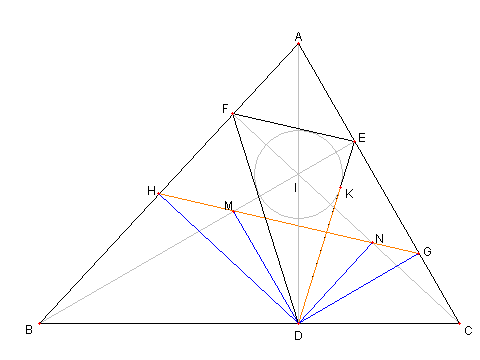
垂心と垂線
図において
D, E, F は ⊿ABC の頂点 A, B, C から
各々辺 BC, CA, AB に引いた垂線の足
H, G, M, N は点 D より
AB, AC, BE, CF に引いた垂線の足
I は ⊿ABC の内心から DE に引いた
垂線の足とする
このとき、次を示せ
① H, M, N, G は同一直線上にある
② FE と HG は平行である
③ MN = DK である
解説 Applet版
|
|
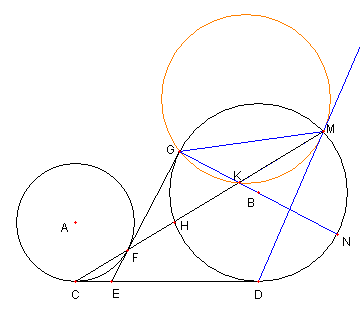
|
外接線と内接線と割線
図のように
円 A 上の点 C, F と円 B 上の点 D, G を
CD が二円の共通外接線、
FG が二円の共通内接線
であるようにとる
E は CD と FG との交点とする。
直線 CF と円 B との交点を H, M とする。
GN を円 B の直径とする。
HM と GN と交点を K とする。このとき
GM が ⊿GKM の外接円と接していることを示せ
解説 Applet版
|
|
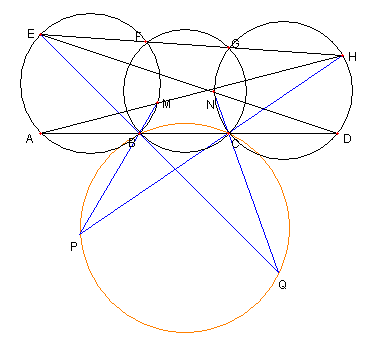
|
4つ目の外接円
図において
A, B, C, D は一直線上にある
E, F, G, H は一直線上にある
A, B, M, F, E は同一円周上にある
B, C, G, F は同一円周上にある
C, D, H, G, N は同一円周上にある
A, M, H は一直線上にある
E, N, D は一直線上にある
P は二直線 MB と HC との交点
Q は二直線 NC と EB との交点
とする。このとき次を示せ
B, P, Q, C は同一円周上にある
解説 Applet版
|
|
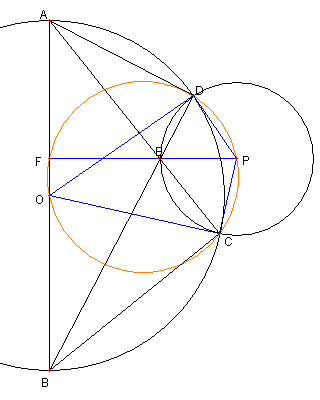
|
直径と二つの弦と二つの外接円
AB を直径とする円の
二本の弦 AC と BD が円内の点
E で交わっている。
P を ⊿CDE の外心とし
AB と PE の延長との交点を F とする。
このとき P, D, F, O, C が
同一円周上にあることを示せ。
解説 Applet版
|
|
|
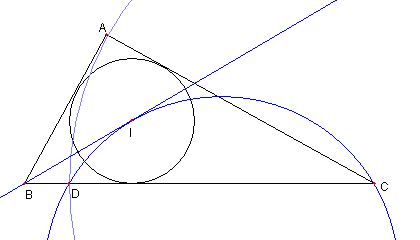
直角三角形と内心
⊿ABC は ∠BAC = 90°の直角三角形として
I はその内心とする
D は BC 上の点で CD = CAとする
このとき、次を示せ
① BI は ⊿IDC の外接円に接している
② BI2 = a(a-b)
③ BI2 : CI2 = a-b : a-c
ここで
a = BC, b = CA, c = AB としている。
解説 Applet版
|
|
|
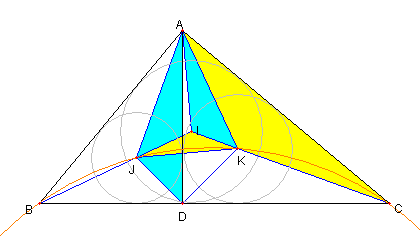
直角三角形と垂線と内接円と相似
⊿ABC は ∠BAC = 90°の直角三角形
D は A から BC に下ろした垂線の足
I, J, K は各々 ⊿ABC, ⊿ABD, ⊿ADC の
内心 とする。このとき次を示せ
① ⊿AJD ∽ ⊿AIK である。
② B, C, K, J は同一円周上にある
③ ⊿IJK ∽ ⊿KCA である。
④ ⊿DJK ∽ ⊿ABC である。
解説 Applet版
|
|
|
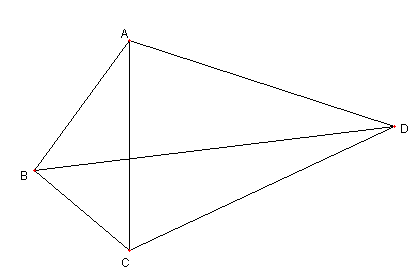
角度の問題
図において
∠BAC = 36°, ∠BCA = 50°
∠CAD = 72°, ∠ACD = 65° のとき
∠BDC を求めよ
一般問題と解説 Applet版
|
|
|
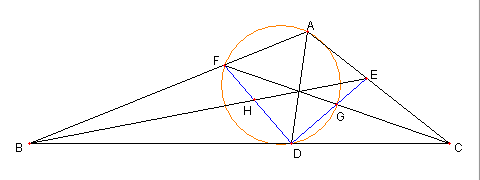
120°の鈍角三角形と角の二等分線
⊿ABC は ∠BAC が120°の鈍角三角形とする。
D, E, F は各々辺 BC, CA, AB 上の点で
AD, BE, CF は各々
∠BAC, ∠CBA, ∠ACB の二等分線とする。
DE と CF との交点を G とし
DF と BE との交点を H とする
このとき、次を示せ
① ∠CED = 30°
② H は ⊿ABD の内心である
③ A, F, D, G は
FG を直径とする円の円周上にある
解説 Applet版
|
|
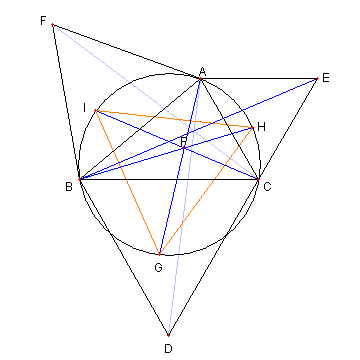
|
4つの正三角形
⊿ABC の各辺を一辺とする三つの正三角形
⊿AFB, ⊿BDC, ⊿CEA を描く
図のように点 P を
⊿PBC ∽ ⊿ABE
となるようにとる。このとき次を示せ
① ⊿PCA ∽ ⊿BCF
② ⊿PAB ∽ ⊿CAD
③ AP, BP, CP それぞれの延長との
交点を G, H, I とおくと
⊿GHI は正三角形である。
解説 Applet版
|
|
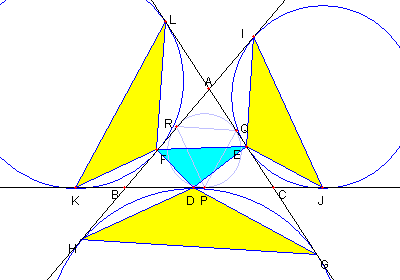
|
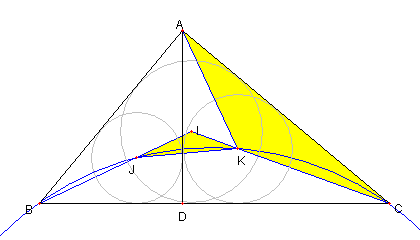
傍接円と4つの三角形の問題
⊿ABC の三つの傍接円と各辺との接点を
図のように
D, G, G, E. I, J, F, K, L とする。
⊿ABC、⊿DEF, ⊿DGH, ⊿EIJ, ⊿FKL の面積を
各々 T, S, Sa, Sb, Sc とおくとき
① S/T = 2αβγ/(abc)
② Sa/T = 2sβγ/(abc)
③ Sb/T = 2sαγ/(abc)
④ Sc/T = 2sαβ/(abc)
⑤ S/Sa = α/s, S/b = β/s,
S/c = γ/s
1/Sa + 1/Sb + 1/Sc = 1/s
⑥ ⊿PQR の面積 = ⊿DEF の面積
ここで
a = BC, b = CA, c = AB
s = (a + b + c)/2
α = s - a, β = s - b, γ = s - c
としている。
解説 Applet版
|
|
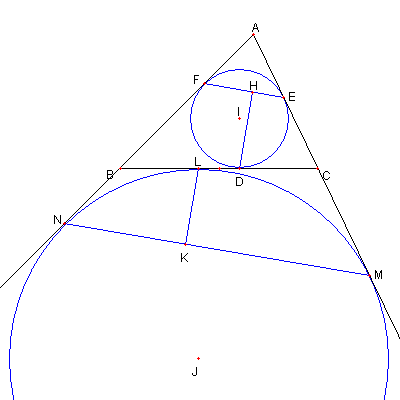
|
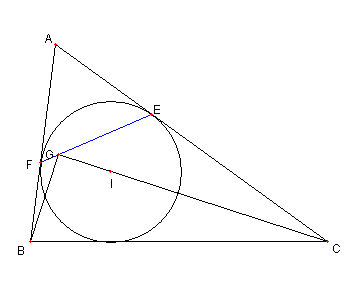
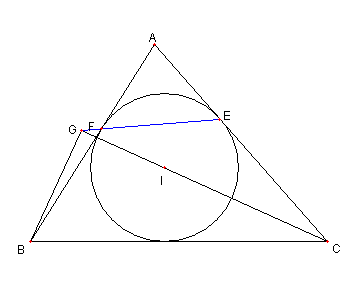
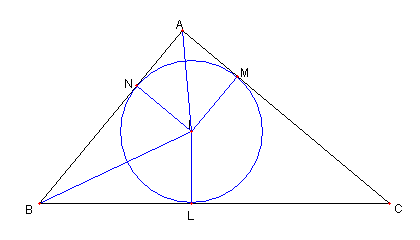
問題 内接円と傍接円
⊿ABC が与えられている
⊿ABC の内接円と、辺 BC, CA, AB との
各々の接点を D, E, F とおく
⊿ABC の傍接円と、辺 BC, CA, AB (延長)との
各々の接点を L. M,N とおく
D から EF に下ろした接線の足を H とし
L から MN に下ろした接線の足を K とする
このとき
DH = LK
であることを示せ
解説 Applet版
|
|
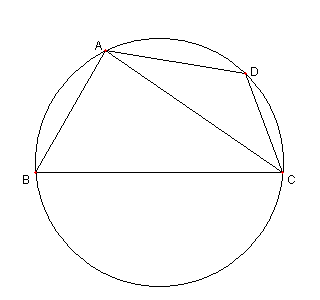
|
問題
四辺形 ABCD は円に内接しており
AB = AD = 4, AC = root(37)
四辺形 ABCD の面積 = 10 root(3)
BC ≥ CD
とする。このとき
BC の長さを求めよ。
数学博物館すうじあむ
にあった問題です
解説 Applet版
|
|
|
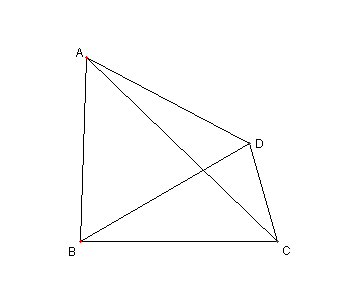
問題
図において
AB = AC = AD
E は ⊿ABD の外接円と
AC との交点とする。
このとき
ED = EC
である。
解説 Applet版
|
|
|
問題
I を ⊿ABC の内心とする
⊿ABC の内接円と辺 AC, AB との接点を
各々 E, F とする。
B から直線 CI に下ろした垂線の足を
G とおく
このとき
E, F, G が一直線上にあることを示せ
解説 Applet版
|
|
|
問題
I を ⊿ABC の内心とする
⊿ABC の内接円と辺 AC, AB との接点を
各々 E, F とする。
B から直線 CI に下ろした垂線の足を
G とおく
このとき
E, F, G が一直線上にあることを示せ
前問題の G の位置が異なる場合
解説 Applet版
|
|
|
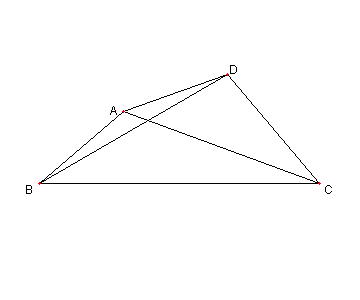
問題
図において
∠DBC = 30°,
∠ACB = 44°, ∠ACD = 30°
AB = AD
とする。このとき
∠BAC を求めよ
解説 Applet版
|
|
|
問題
図において
∠DBC = 30°,
∠ACB = 20°, ∠ACD = 30°
AB = AD
とする。このとき
∠BAC を求めよ
解説 Applet版
|
|
|
問題
図において
⊿ABC は
∠BAC = 80°, AB = AC
の二等辺三角形であり
D は B から AC に引いた垂線の足
E は AD 上の点で
EA = EB
とする。このとき
∠ACE = 30°
であることを示せ
解説 Applet版
|
|
|
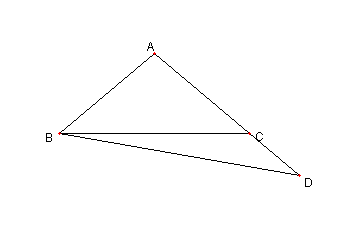
問題
⊿ABC は AB = AC の二等辺三角形で
D は AD の延長線上の点で
∠ADB = 30°
とする。このとき
∠BAC を求めよ
解説 Applet版
Topに戻る
|
|
|

|
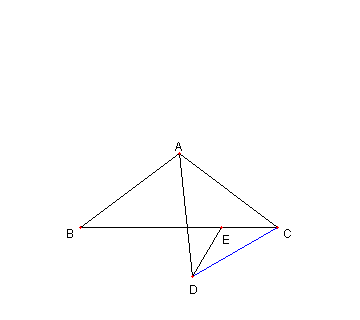
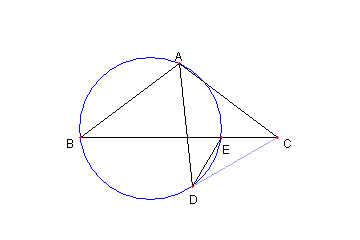
問題
図において
AB = AC = AD
E は ⊿ABD の外接円と
AC との交点とする。
このとき
ED = EC
である。
|
|
|
∠ECD = ∠EDC を示す。
その為に
2∠ECD = ∠BED を示す。
|
|
|
∠BED = ∠BAD である。
|
|
|
2∠BCD = ∠BAD である。
戻る
|
|

|
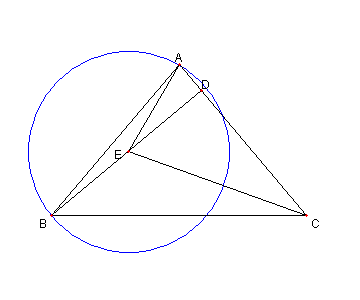
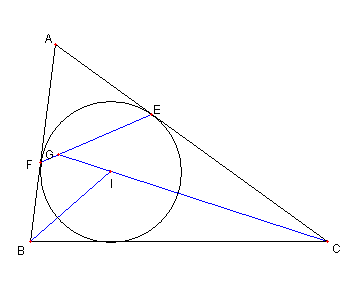
問題
I を ⊿ABC の内心とする
⊿ABC の内接円と辺 AC, AB との接点を
各々 E, F とする。
直線 CI と EF との交点を
G とするとき
∠BGC = 90°を示せ。
これをとくとよい
|
|
|
∠EGC =∠FBI を示す
|
|
|
∠IEF = ∠IAC に注目する
∠IAC + ∠ACG + ∠ABI
= (∠BAC + ∠ACB + ∠ABC)/2
= 90°
なので
∠EGC = ∠AEF - ∠ACG
= 90°- ∠IEF - ∠ACG
= 90°- ∠IAC - ∠ACG
= ∠ABI
|
|
|
∠EGC =∠FBI なので
四辺形 FBIG は円に内接している
よって
∠BGI = ∠BFI = 90°がわかる
戻る
|
|

|
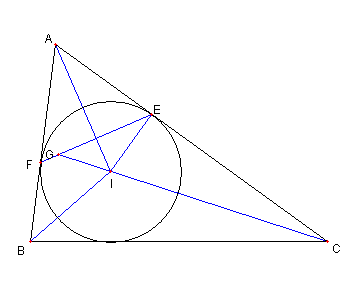
問題
I を ⊿ABC の内心とする
⊿ABC の内接円と辺 AC, AB との接点を
各々 E, F とする。
直線 CI と EF との交点を
G とするとき
∠BGC = 90°を示せ。
これをとくとよい
|
|
|
∠EGC =∠FBI を示す
|
|
|
∠IEF = ∠IAC に注目する
∠IAC + ∠ACG + ∠ABI
= (∠BAC + ∠ACB + ∠ABC)/2
= 90°
なので
∠EGC = ∠AEF - ∠ACG
= 90°- ∠IEF - ∠ACG
= 90°- ∠IAC - ∠ACG
= ∠ABI
|
|
|
∠EGC =∠FBI なので
四辺形 FBIG は円に内接している
よって
∠BGI = ∠BFI = 90°がわかる
戻る
Topに戻る
|
|

|
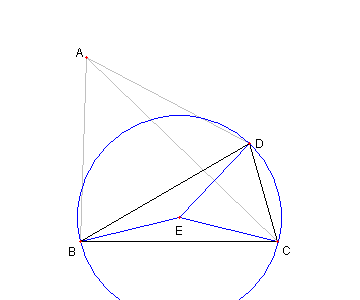
問題
図において
∠DBC = 30°,
∠ACB = 44°, ∠ACD = 30°
AB = AD
とする。このとき
∠BAC を求めよ
|
|
|
⊿BCD の外心を E とおく
EC = ED であり
∠CED = 2∠CBD = 60°なので
⊿CDE は正三角形である
∠ACD = 30°,∠ACB = 44°, ∠ACE = 60 °なので
∠ECB = 14°である。
∠CBD = 30°なので
∠EBC = ∠ECB = 14°
∠EDB = ∠EBD = 16°である
|
|
|
より
AD = AE、∠EAC = ∠DAC である
AB = AD だったので
B, D, E は A を中心とする円の
円周上にある。
∠BAE = 2∠BDE = 32°
∠EAD = 2∠EBD = 32°
∠EAC = ∠DAC なので
∠BAC = 48°である
戻る
|
|
|

|
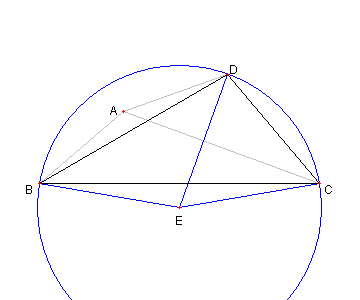
問題
図において
∠DBC = 30°,
∠ACB = 20°, ∠ACD = 30°
AB = AD
とする。このとき
∠BAC を求めよ
|
|
|
⊿BCD の外心を E とおく
∠CED = 2∠CBD = 60° である。
よって
∠ECB = 60°- ∠DCB = 10°
故に
∠EBC = ∠ECB = 10°
∠CBD = 30°なので
∠EDB = ∠EBD = 40°
である。
|
|
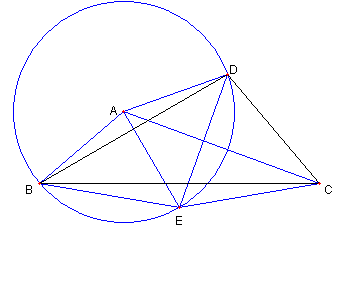
|
EC = ED, ∠CED = 60°
より ⊿CDE は正三角形である
∠DCE = 60°、∠ACD = 30°なので
AC は ED を直交二等分する
よって
AE = AD で ∠EAC = ∠DAC
である。
AB = AD だったので
B, D, E は A を中心とする円の
円周上にある。
∠BAE = 2∠BDE = 80°
∠EAD = 2∠EBD = 80°
∠EAC = ∠DAC なので
∠BAC = 120°である
戻る
Topに戻る
|
|
|

|
図において
⊿ABC は
∠BAC = 80°, AB = AC
の二等辺三角形であり
D は B から AC に引いた垂線の足
E は AD 上の点で
EA = EB
とする。このとき
∠ACE = 30°
であることを示せ
|
|
|
題意の図を
解答が得られる形で作図しよう
∠AEB = 160°, EA = EB
の二等辺三角形 ⊿EAB を描く
|
|
|
∠BEG = 80°, EB = EG
の二等辺三角形 ⊿EBG を描く
|
|
|
∠BGC = 160°, GB = GC
の二等辺三角形 ⊿GBC を描く
|
|
|
⊿ABC ∽ ⊿EBG
がわかり
∠BAC = 80°, AB = AC
がわかる
|
|
|
BE の延長と AC との交点を D とおく
∠ABE = 10°なので ∠EBC = 40°である。
∠ACB = 50°なので ∠BDC = 90°
つまり D は B から AC に下ろした垂線の足である。
|
|
|
DC 上に点 F を
DF = AD となるようにとる。
∠AEF = 60°で EF = EA である。
|
|
|
A, B, G, F は E を中心とした円の円周上にあり
∠GEF = 360° - 40 °- 160° - 80°
= 80°= ∠BEG
なので
GB = GF
|
|
|
∠GCF = 60°で GC = GFなので
⊿GCF は正三角形である。
|
|
|
EF = EG, CF = CG, ∠FCG = 60°
でなので
∠FCE = 30°である
|
|
|
図において
∠BAC = 80°, AB = AC
D は B から AC に引いた垂線の足
E は AD 上の点で
EA = EB であり
∠ACE = 30°である
戻る
Topに戻る
|
|
|

|
⊿ABC は AB = AC の二等辺三角形で
D は AD の延長線上の点で
∠ADB = 30°
とする。このとき
∠BAC を求めよ
|
|
|
題意の図を
E を ⊿ABD の外心とする
EA = EB = ED であり
∠AEB = 2∠ADB = 60°である。
EA = EB, ∠AEB = 60°より
⊿ABE は正三角形である
|
|
|
⊿ABC と ⊿EDA において
AB = ED, AC = EA, BC = DA より
⊿ABC ≡ ⊿EDA である
これらの二等辺三角形の低角を α とおくと
∠BAC = 180°- 2α
∠BAC = 60°+ α
従って α = 40°を得て
∠BAC = 100°を得る。
戻る
Topに戻る
|
|
|

|
問題
四辺形 ABCD は円に内接しており
AB = AD = 4, AC = root(37)
四辺形 ABCD の面積 = 10 root(3)
BC ≥ CD
とする。このとき
BC の長さを求めよ。
数学博物館すうじあむ
にあった問題です
|
|
s = 10 root(3), c = root(37)
b = BC, d = CD
とおく。
AB = AD より
∠ACB = ∠ACD である。
これを θ とおく
余弦定理より
AB2 = AC2 + BC2 - 2AC×BC cos θ
AD2 = AC2 + CD2 - 2AC×CD cos θ
より。
① 16 = 37 + b2 - 2bc cos θ
② 16 = 37 + d2 - 2dc cos θ
これらより
2(b-d)c cos θ = b2 - d2
(b ≠ d より)
③ b+d = 2c cos θ
四角形 ABCD の面積計算して
bc sin θ + dc sin θ = 2s
つまり
④ (b+d)c sin θ = 2s
c2 = 37 より ④ に ③ を代入して
⑤ 37 sin 2θ = 2s
|
これより
c cos θ = 5
①、② より b, d は方程式
x2 - 10x + 21 = 0
の解である。
b ≥ d より b = 7, d = 3 である。
b ≠ d の理由
もし b = d とすると
∠ABD = 90 °なり b = root(21) = d を得て
四角形 ABCD の面積 = 4 root(21) となり矛盾
途中に戻る
|
|

|
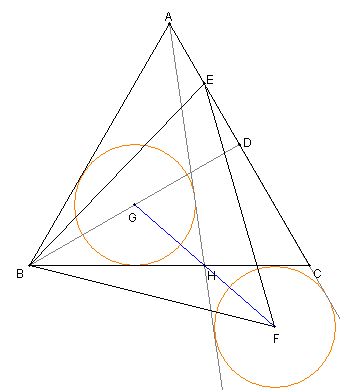
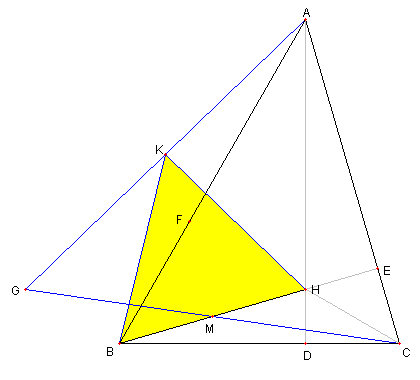
問題 内接円と傍接円
⊿ABC が与えられている
⊿ABC の内接円と、辺 BC, CA, AB との
各々の接点を D, E, F とおく
⊿ABC の傍接円と、辺 BC, CA, AB (延長)との
各々の接点を L. M,N とおく
D から EF に下ろした接線の足を H とし
L から MN に下ろした接線の足を K とする
このとき
DH = LK
であることを示せ
|
|
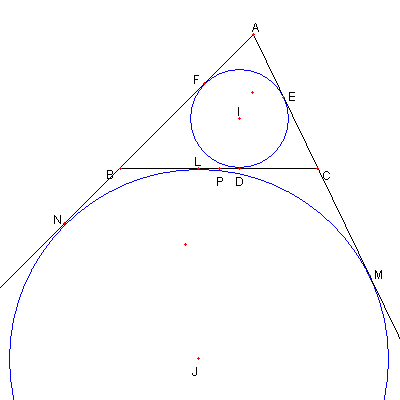
|
P を BC の中点とする。
次に注意する。
① AE = AF, AN = AM
② BF = BD = CL = CM
③ CE = CD = BL = BN
④ LP = PD
|
|
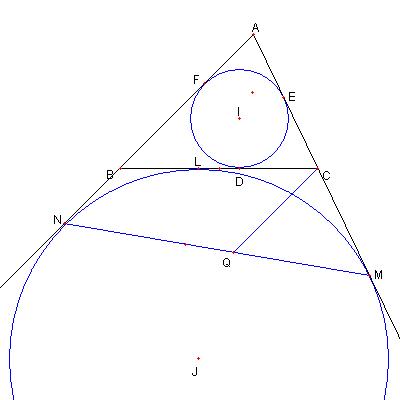
|
C を通り AB と平行な直線と MN との交点を
Q とおく
|
|
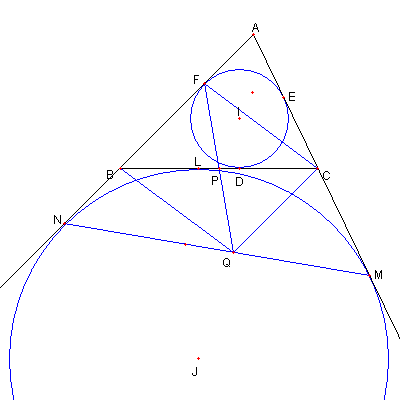
|
⊿ANM ∽ ⊿CQN で AN = AM なので
CQ = CM
である
CQ = FB (②を使った) で
FB と CQ は平行なので
四辺形 FBQC は平行四辺形
よって BC の中点 P は FQ の中点である
|
|
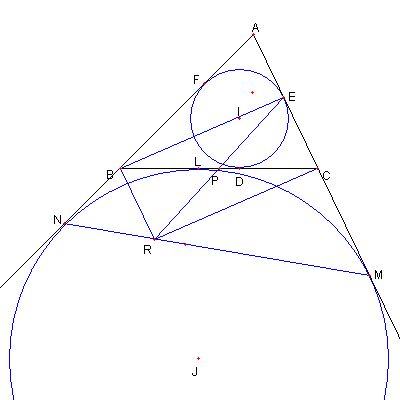
|
B を通り AC と平行な直線と MN との交点を
R とおく
上と同様な議論により
P は ER の中点である
|
|
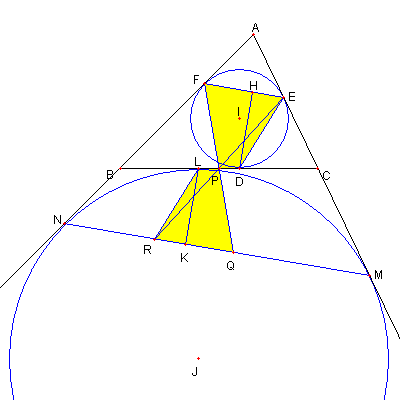
|
P は線分 DL, ER, FQ の中点なので
四辺形 PDEF と PLRQ は
P に関して点対称であるよって
D から EF の高さと
R から RQ への高さは等しい
つまり DH = LK である。
問題に戻る
Topに戻る
|
|
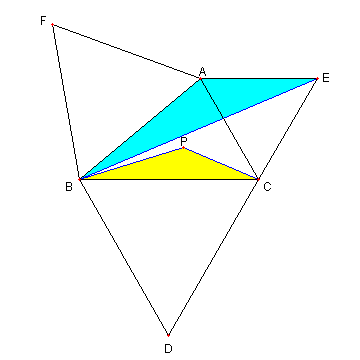
|
⊿ABC の各辺を一辺とする三つの正三角形
⊿AFB, ⊿BDC, ⊿CEA を描く
図のように点 P を
⊿PBC ∽ ⊿ABE
となるようにとる。
|
|
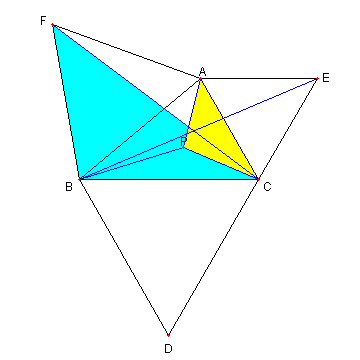
|
このとき次を示せ
① ⊿PCA ∽ ⊿BCF
|
|
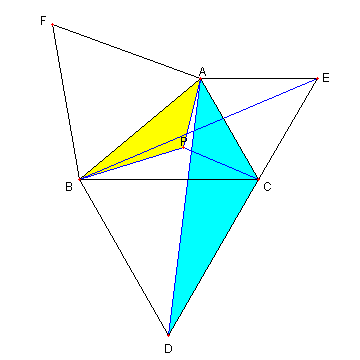
|
② ⊿PAB ∽ ⊿CAD
|
|

|
⊿ABC の外接円と
③ AP, BP, CP それぞれの延長との
交点を G, H, I とおくと
⊿GHI は正三角形である。
|
|
|
④ AD, BE, CF は一点で交わる
交点を Q とおく
⑤ ⊿ABE ≡ ⊿AFC
⊿BCF ≡ ⊿BDA
⊿CAD ≡ ⊿CEB
|
|
① ⊿PCA ∽ ⊿BCF の説明
⊿PBC ∽ ⊿ABE より
∠PCB = ∠AEB
⑤ より ∠AEB = ∠ACF
よって ∠PCA = ∠BCF
⊿PBC ∽ ⊿ABE より
BC : PC = BE : AE
よって
AE : PC = BE : BC
仮定より AE = CA, ⑤ より BE = CF なので
CA : PC = CF : BC
∠PCB = ∠AEB だったので
⊿PCA ∽ ⊿BCF
同様に ② も示せる
問題に戻る
Topに戻る
|
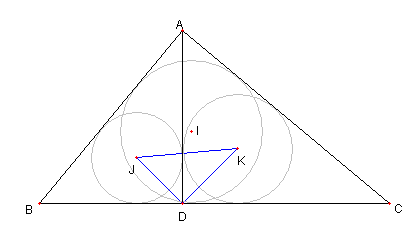
傍接円と4つの三角形の問題

|
⊿ABC の三つの傍接円と各辺との接点を
図のように
D, G, G, E. I, J, F, K, L とする。
⊿ABC、⊿DEF, ⊿DGH, ⊿EIJ, ⊿FKL の面積を
各々 T, S, Sa, Sb, Sc とおくとき
① S/T = 2αβγ/(abc)
② Sa/T = 2sβγ/(abc)
③ Sb/T = 2sαγ/(abc)
④ Sc/T = 2sαβ/(abc)
⑤ S/Sa = α/s, S/b = β/s,
S/c = γ/s
1/Sa + 1/Sb + 1/Sc = 1/s
⑥ ⊿PQR の面積 = ⊿DEF の面積
ここで
a = BC, b = CA, c = AB
s = (a + b + c)/2
α = s - a, β = s - b, γ = s - c
としている。
|
|
定義より
AL = AF, AI = AE、AH = AG
BK = BF, BH = BD, BJ = BI
CG = CD, CJ = CE, CL = CK
である
よって
2AH = AH + AG = AB + BH + AC + CG
= AB + BD + AC + CD
= AB + BC + CA = c + a + b = 2s
より
AG = AH = s
同様にして、次を得る
AG = AH = BI = BJ = CK = CL = s
よって
BF = BK = CK - BC = s - a = α
CE = CJ = BJ - BC = s - a = α
同様に
AF = AL = CD = CG = s - b = β
BD = BH = AE = AI = s - c = γ
また
a = β + γ, b = γ + α c = α + β
s = α + β + γ
ある
|
|
⊿AEF の面積/T = AE×AF/(AC×AB)
= βγ/(bc)
同様に
⊿BFD の面積/T = γα/(ca)
⊿CDE の面積/T = αβ/(ab)
よって
S/T = 1 - βγ/(bc)1 - γα/(ca) - αβ/(ab)
である。ゆえに
abc - aβγ - bγα - cαβ
=
(β + γ)(γ + α)(α +. β)
- (β + γ)βγ
- (γ + α)γα
- (α +. β)αβ
= 2αβγ
なので
S/T = 2αβγ/(abc)
|
|
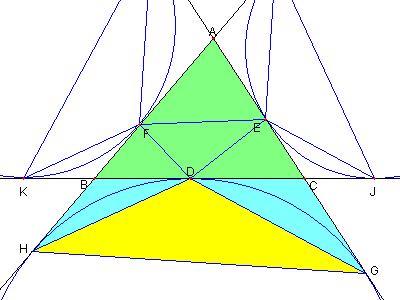
|
⊿AHG の面積/T = AG×AH/(AC×AB) = s2/(bc)
⊿BDH の面積/T = γ2/(ca)
⊿CDG の面積/T = β2/(ab) より
Sa/T = s2/(bc) - 1 - γ2/(ca) -
β2/(ab) である
as2 - abc =
as2 - a(s - β)(s - γ)
= asγ + asβ - aβγ
,
aβγ + bγ2 + cβ2
= (β + γ)βγ + (s - β)γ2 +
(s - γ)β2
= s(γ2 + β2)
なので
as2 - abc - bγ2 - cβ2
=
asγ + asβ - s(γ2 + β2)
=
s((β + γ)(β + γ) - γ2 - β2)
= 2sβγ
故に Sa/T = 2sβγ/(abc)
|
|
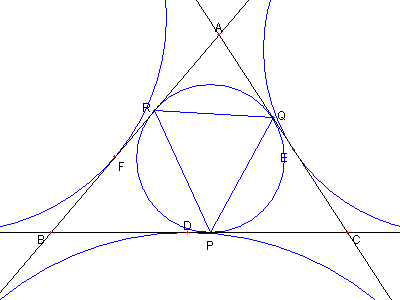
|
AP = AR = α, BP = BR = β, CQ = CP = γ
である。
⊿PQR の面積/T
= 1 - α2/(bc) -
β2/(ca) - γ2/(ab)
である
abc - aα2 - bβ2 -cγ2
=
(β + γ)(γ + α)(α +. β)
- (β + γ)α2
- (γ + α)β2
- (α +. β)γ2
= 2αβγ
なので
⊿PQR の面積/T = 2αβγ/(abc) = S/T
よって
⊿PQR の面積 = ⊿DEF の面積
問題に戻る
Topに戻る
|

|
120°の鈍角三角形と角の二等分線
⊿ABC は ∠BAC が120°の鈍角三角形とする。
D, E, F は各々辺 BC, CA, AB 上の点で
AD, BE, CF は各々
∠BAC, ∠CBA, ∠ACB の二等分線とする。
DE と CF との交点を G とし
DF と BE との交点を H とする
このとき、次を示せ
① ∠CED = 30°
② H は ⊿ABD の内心である
③ A, F, D, G は
FG を直径とする円の円周上にある
|
|
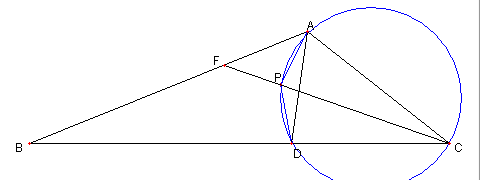
|
④ ∠PAD = ∠PCD = ∠PCA = ∠PDA
⑤ ∠PFA = 60°- ∠ACP
= 60°- ∠PAD = PAF
を示す
|
|
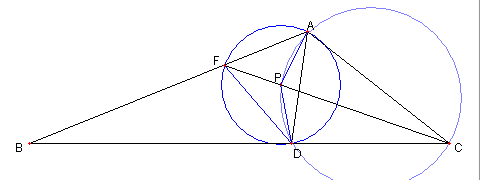
|
PA = PD = PF より
A, F, D は P を中心とする円の円周上にある。
よって
∠DPC = ∠DAC = 60°なので
∠DFC = ∠DPC/2 = 30°である。
① が示せた
|
|
|
∠PDA = ∠PCD
∠PDF = ∠PFD
∠FDB = ∠CFD + ∠FCD
なので
∠FDB = ∠FDA
DF が ∠ADB の二等分線であり
BE が ∠ABD の二等分線なので
H は ⊿ABD の内心である
②が示せた
|
|
|
② により、G が
⊿ADC の内心であることがわかる。
DF が∠ADB の二等分線であり
DE が∠ADC の二等分線なので
∠FDG = 90°である
AG が∠の二等分線なので
∠DAG = 30°である
∠BAD = 60°なので
∠FAG = 90°である
以上より A, D が FG を直径とする
円の円周上にあることがわかる
問題に戻る
Topに戻る
|
|
|

|
角度の問題
∠BAC = 2α, ∠BCA = 2β
∠CAD = 90°- α, ∠ACD = 90°- β のとき
∠BDC = α であることを示せ
こちらの方が一般であり
易しい問題になります。
|
|
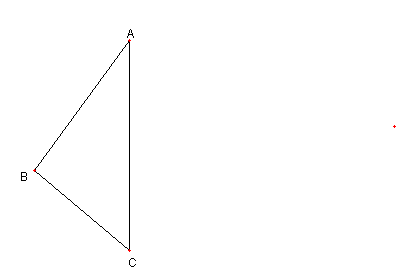
|
題意の図は相似の意味で
一意的に定まるので
答えがわかるように題意の図を作図します
∠BAC = 2α, ∠BCA = 2β
の ⊿ABC を作図します
|
|
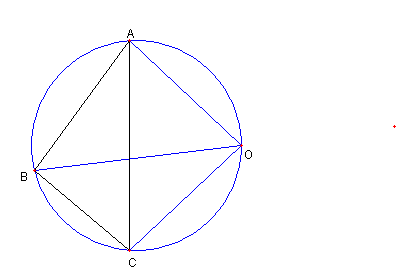
|
図のように
⊿ABC の外接円上に点 O を
OA = OC
となるようにとる。
∠BOC = ∠BAC = 2α, ∠BOA = ∠BCA = 2β で
∠AOC = ∠AOB + ∠BOC = 2α + 2β であり
∠OAC = ∠OCA = 90°- α - β である。
|
|
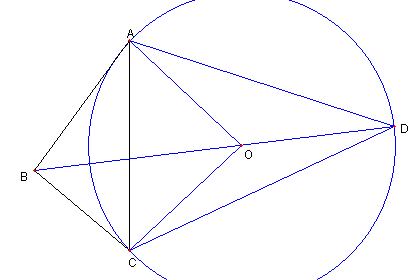
|
BO の延長上に点 D を
OD = OA = OC となるようにとる。
このとき
∠OAD = ∠ODA = ∠AOB/2 = β
∠OCD = ∠ODC = ∠BOC/2 = α である
∠OAC = ∠OCA = 90°- α - β だったので
∠CAD = 90°- α, ∠ACD = 90°- β である
そして
∠BDC = α である
問題に戻る
Topに戻る
|
|
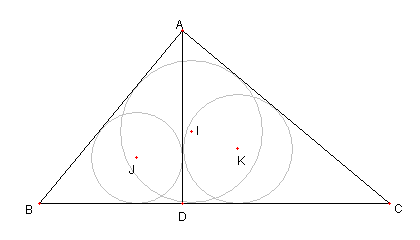
|
直角三角形と垂線と内接円と相似
⊿ABC は ∠BAC = 90°の直角三角形
D は A から BC に下ろした垂線の足
I, J, K は各々 ⊿ABC, ⊿ABD, ⊿ADC の
内心 とする。このとき次を示せ
|
|
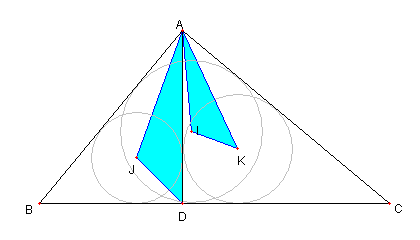
|
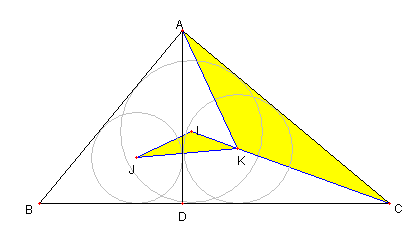
① ⊿AJD ∽ ⊿AIK である。
|
|
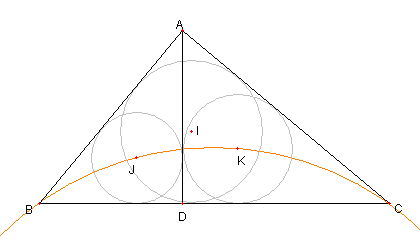
|
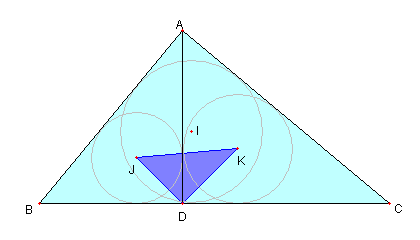
② B, C, K, J は同一円周上にある
|
|
|
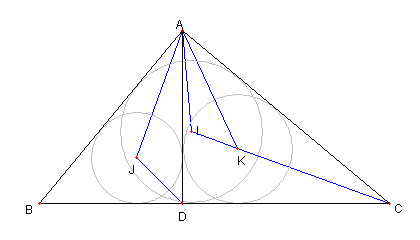
③ ⊿IJK ∽ ⊿KCA である。
|
|
|
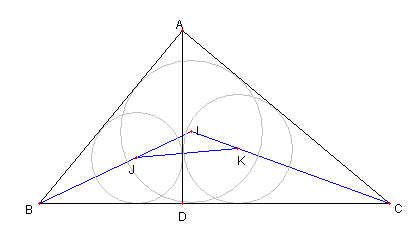
④ ⊿DJK ∽ ⊿ABC である。
|
|
|
① について
∠IAC = 45°= ∠JDA
∠IKA = ∠KAC + ∠KCA = 45°
∠KCA = ∠DAC なので
∠JDA = 45°= ∠IKA
∠JAD = ∠ICA = 45°- ∠KAC = ∠IAK
従って
⊿AJD ∽ ⊿AIK である。
|
|
|
② について
a = BC, b = CA, c = AB
q = BI/BC, r = CK/BC
とおく
BI = aq, CI = ar
AK = bq, CK = br
BJ = cq, AJ = cr であり
IJ×IB = (aq-cq)×aq
IK×IC = (ar-br)×ar である
次に示すように
(a-c)aq2 = (a-b)ar2 なので
IJ×IB = IK×IC
よって B, C, K, J は同一円周上にある。
|
|
(a-c)aq2 = (a-b)ar2 の証明
L, M, N を各々 I から辺 BC, CA, AB に
下ろした垂線の足とする
四辺形 ANIM は正方形であり。
BN = (a + c - b)/2
IN = AN = (b + c - a)/2 である
IB2 = BN2 + IN2 なので
4(aq)2 = 4IB2 =
(a + c - b)2 + (b + c - a)2
= 2c2 + 2(a-b)2
= 2a2 + 2b2 + 2c2 - 4ab
= 4a2 - 4ab = 4a(a-b)
つまり
aq2 = (a-b)
同様に ar2 = (a-c)
直角三角形と内心 を使うほうが簡単でした
|
|
③ について
B, C, K, J が同一円周上にあるので
⊿IJK ∽ ⊿ICB
明らかに ⊿ICB ∽ ⊿KCA なので
⊿IJK ∽ ⊿KCA である。
|
|
|
④ について
DJ, DK は各々
∠BDA, ∠ADC の二等分線なので
∠JDK = 90°である。
DJ : DK = DB : DA = AB : AC である。
よって
⊿DJK ∽ ⊿ABC である。
問題に戻る
Topに戻る
|
|

|
直角三角形と内心
⊿ABC は ∠BAC = 90°の直角三角形として
I はその内心とする
D は BC 上の点で CD = CAとする
このとき、次を示せ
① BI は ⊿IDC の外接円に接している
② BI2 = a(a-b)
③ BI2 : CI2 = a-b : a-c
ここで
a = BC, b = CA, c = AB としている。
|
|
|
E を BI の延長線上の点とする。
∠ABC + ∠ACB = 90°で
IB は ∠ABC の二等分線で
IC は ∠ACB の二等分線なので
∠EIC = 45°である。
IA は ∠BAC の二等分線なので
∠IAC = 45°
⊿IDC ≡ ⊿IAC なので
∠IDC = ∠IAC
よって
∠EIC = 45°= ∠IDC
故に EI は ⊿IDC の外接円に接している。
②、③ は ① の直接の結果
問題に戻る
Topに戻る
|
|

|
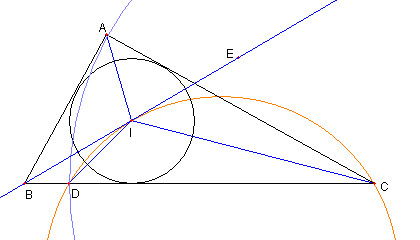
直径と二つの弦と二つの外接円
AB を直径とする円の
二本の弦 AC と BD が円内の点
E で交わっている。
P を ⊿CDE の外心とし
AB と PE の延長との交点を F とする。
このとき P, D, F, O, C が
同一円周上にあることを示せ。
|
|
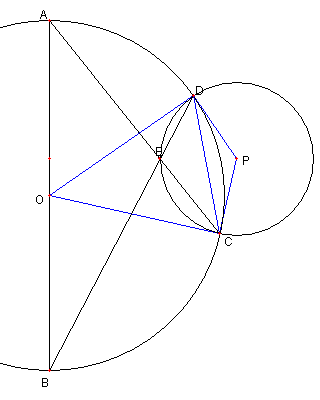
|
PO が当該の円の直径であることを示す
つまり
∠PCO = ∠PDO = ∠PFO = 90°を示す。
∠ACO = ∠BAC = ∠BDC なので
OC は ⊿CDE の外接円の接点である
よって ∠PCO = 90°である
同様に ∠PDO = 90°である。
|
|
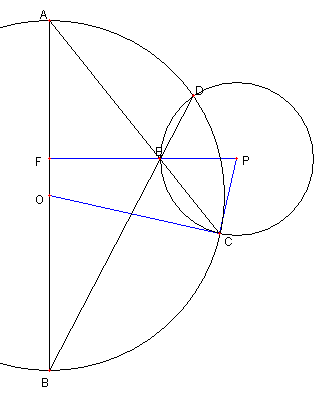
|
∠FAE + ∠AEF = ∠ACO + ∠PEC
= ∠ACO + ∠PCE = ∠PCO = 90°
なので
∠AFE = 90°である。
問題に戻る
Topに戻る
|
|
|

|
4つ目の外接円
図において
A, B, C, D は一直線上にある
E, F, G, H は一直線上にある
A, B, M, F, E は同一円周上にある
B, C, G, F は同一円周上にある
C, D, H, G, N は同一円周上にある
A, M, H は一直線上にある
E, N, D は一直線上にある
P は二直線 MB と HC との交点
Q は二直線 NC と EB との交点
とする。このとき次を示せ
B, P, Q, C は同一円周上にある
|

|
∠PBQ = ∠PCQ を示す
その為に
∠EBM = ∠HCN を示す
|
|
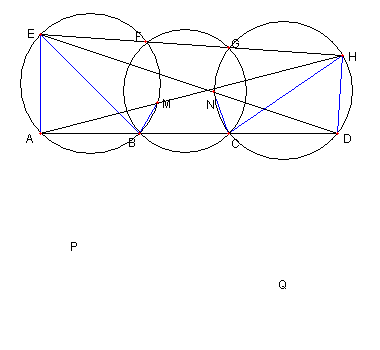
|
その為に
∠EAM = ∠HDN を示す
|
|
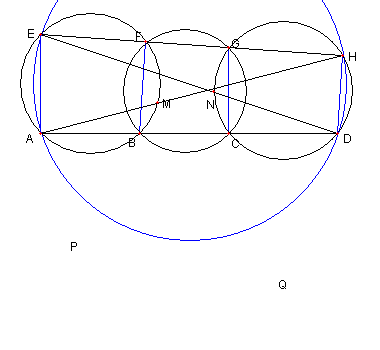
|
その為に
∠EAH = ∠HDE を示す
これは
∠AEF = ∠FBC = ∠GH なので
∠AEH + ∠ADH = ∠CBH + ∠CDH = 180°
よって四辺形 EADH が円に内接しているので
示せる。
問題に戻る
Topに戻る
|

|
外接線と内接線と割線
図のように
円 A 上の点 C, F と円 B 上の点 D, G を
CD が二円の共通外接線、
FG が二円の共通内接線
であるようにとる
E は CD と FG との交点とする。
直線 CF と円 B との交点を H, M とする。
GN を円 B の直径とする。
HM と GN と交点を K とする。このとき
GM が ⊿GKM の外接円と接していることを示せ
|
|
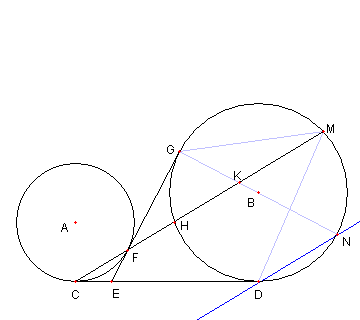
|
① ∠DMC = ∠MGN
を示す
② DN と HM は平行である
これを示す。
これが示せたら 孤HD と孤MN に対応する
円周角が等しいので ①が示せる。
|
|
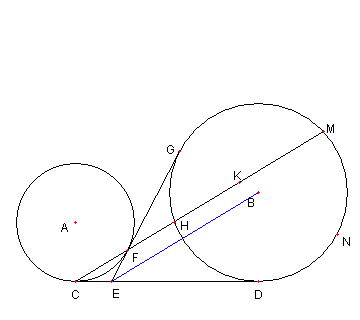
|
③ EB と CM は平行である
これを示す。
EC = EF であり
EB が ∠GED の二等分線なので
CF と EB は平行である
③ が示せた
|
|
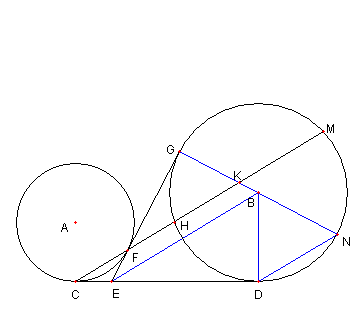
|
④ DN と EB は平行である
これを示す
BD = BN であり
BE が ∠GBD の二等分線なので
DN と EB は平行である
④ が示せた
③、④ より ② が示せる。
問題に戻る
Topに戻る
|
|

|
垂心と垂線
図において
D, E, F は ⊿ABC の頂点 A, B, C から
各々辺 BC, CA, AB に引いた垂線の足
H, G, M, N は点 D より
AB, AC, BE, CF に引いた垂線の足
I は ⊿ABC の内心から DE に引いた
垂線の足とする
このとき、次を示せ
① H, M, N, G は同一直線上にある
② FE と HG は平行である
③ MN = DK である
|
|
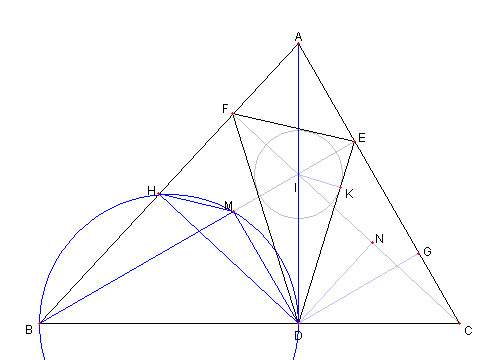
|
∠BHD = 90°= ∠BMD なので
四辺形 HBDM は円に内接している。
よって ∠HMB = ∠HDB
∠DHB = 90°= ∠ADB なので
∠HDB = ∠DAB
よって ∠HMB = ∠DAB
|
|
|
∠AFN = 90°= ∠FND なので
∠DAB = ∠IDN
∠IMD = 90°= ∠IND なので
四辺形 IMDN は円に内接している。
よって ∠IDN = ∠IMN
故に ∠DAB = ∠IMN
∠HMB = ∠DAB だったので
∠HMB = ∠IMN
よって H, M, N は一直線上にある
同様に M, N, G も一直線上にある
① が示せた
|
|
|
∠BEC = 90°= ∠BFC なので
四辺形 FBCE は円に内接している。
よって ∠AFE = ∠ECB
∠BEC = 90°= ∠BMC なので
∠ECB = ∠MDB
四辺形 HBDM は円に内接していたので
∠MDB = ∠AHM
よって ∠AFE = ∠AHM
故に FE と HG は平行である。
|
|
|
∠IMD = ∠IND = ∠IKD = 90°
なので I, M, D, N, K は
ID を直径とする円周上にある。
MN = DK を示すために
∠MDN = ∠KID を示す
|
|
四辺形 IMDN が円に内接しているので
∠MDN = 180°- ∠MIN
∠MIN = ∠FIE である。
四辺形 AFIE が円に内接しているので
∠FAE = 180°- ∠FIN
よって ∠MDN = ∠FAE
∠IKD = 90°なので
∠KID = 90°- ∠IDK
四辺形 IDCE が円に内接しているので
∠IDE = ∠ICE
∠AFC = 90°なので
∠FAE = 90°- ∠FCE
よって ∠KID = ∠FAE
以上より ∠MDN = ∠KID
よって ③ が示せた。
問題に戻る
Topに戻る
|

|
60°の三角形と垂心
⊿ABC において ∠ABC = 60°とする。
H は ⊿ABC の垂心
D, E, F は ⊿ABC の頂点 A, B, C から
各々辺 BC, CA, AB に引いた垂線の足とし
M は BH の中点とする。
CM の延長線上に点 G を
GM = MC となるようにとる。
K を AG の中点とするとき次を示せ。
⊿KBH は正三角である。
|
|
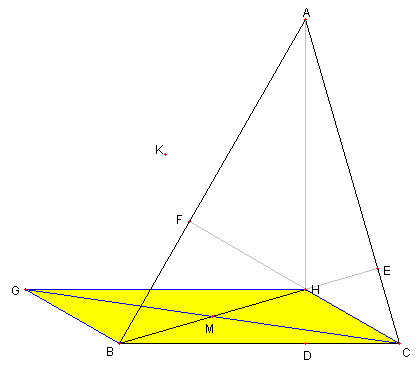
|
BH と CG が互いに他を二等分するので
四辺形 GBCH は平行四辺形である。特に
① GB と HC は平行
② GH と BC は平行
③ ∠HGB = ∠HCB
である
|
|
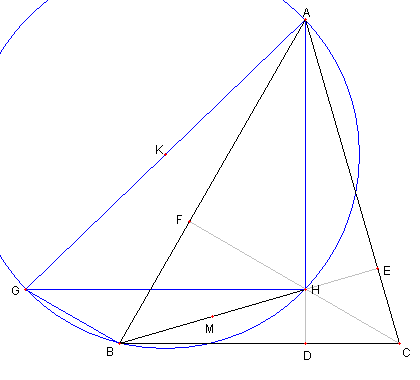
|
AB と CH は直交しているので
① より ∠ABG = 90°
BC と AH は直交しているので
② より ∠AHG = 90°
よって
A, H, B, G は AG を直径とする
円の円周上にある。
|
|
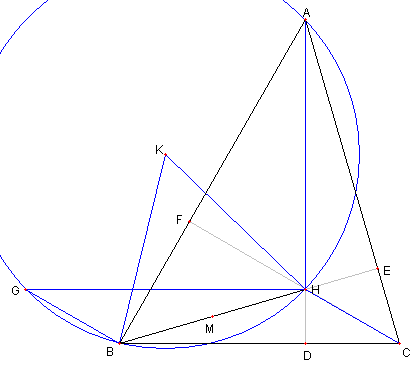
|
∠FCB = 90°- ∠FBC = 30°であるので
③ より ∠HGB = 30°
K は 四辺形 AGBH の外接円の中心なので
∠BKH = 2∠BGK = 60°
よって ⊿KBH は正三角形である
問題に戻る
Topに戻る
|
|

|
角度の問題
図において
AB = AD で ∠ABD = 14°
∠CBD = 16°, ∠CDB = 8°
とするとき
∠BAC = 38°であることを示せ。
(かなりの難問と思います)
解説
|
|
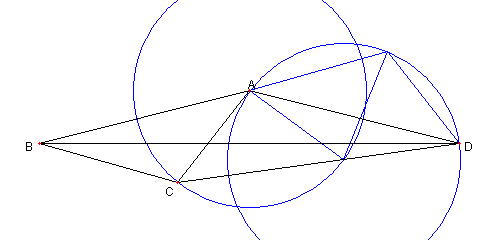
|
相似の意味で一意的に定まるので
答えがわかるように
題意の図を作図しよう
これを、参考にします。
|
|
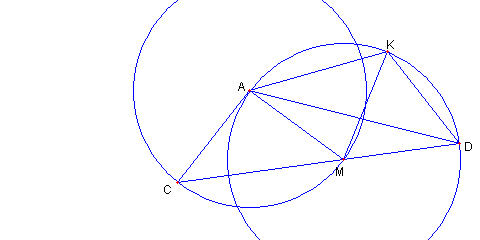
|
正三角形 DKM を画く
MK = MA, ∠AMK = 76°の
二等辺三角形 ⊿MAK を画く
AC = AM, ∠CAM = 92°の
二等辺三角形 ⊿ACM を画く
∠AMC = 44°、∠AMK = 76°、∠KMD = 60°
なので、 C, M, D は一直線上にある
∠ADC = ∠DAM = (∠AMC)/2 = 22°
∠KDA = 60°- ∠ADC = 38°
∠KAD = ∠KAM - ∠DAM = 52°- 22°= 30°
∠CAD = ∠CAM + ∠MAD = 92°+ 22°= 114°
AC = AM = MK = KD
である
|
|
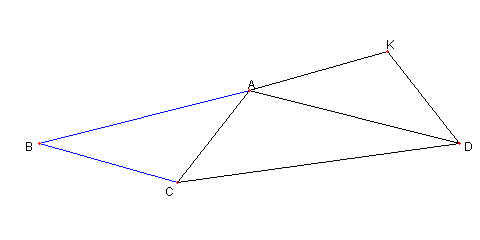
|
AC = KD だった。
図のように点 B を
⊿CAB ≡ ⊿KDA
となるようにとる。
∠CAB = ∠KDA = 38°
AD = AB, ∠BAD = 38°+ 114°= 152°
∠ABC = ∠DAK = 30°
である。
|
|

|
AD = AB, ∠BAD = 38°+ 114°= 152°
なので
∠ABD = ∠ADB = 14°
∠ABC = 30°、∠ABD = 14°より ∠CBD = 16°
∠ADC = 22°、∠ADB = 14°より ∠CDB = 8°
であり、∠BAC = 38°である。
問題に戻る
Topに戻る
|

|
角度の問題((30 + a)°)
図において
D は ⊿ABC の頂点 A から
辺 BC に下ろした垂線の足とする。
∠BAD = (30 + a)°, ∠CAD = (60 + a)°とする
E は AD 上の点で
∠ACE = (30 - 2a)°とする。このとき
∠EBC = 3a°であることを示せ。
(a = 6 の場合が、もとの問題)
一般形です
|
|
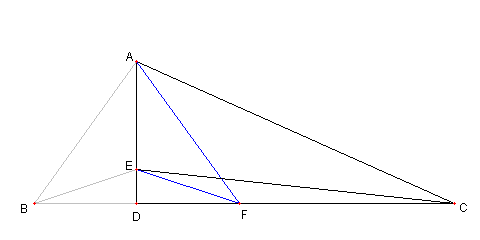
|
補題1
⊿ADE は ∠ADC = 90°の直角三角形で
∠CAD = (60 + a)°とする
F は DC 上の点で ∠DAF = (30 + a)°で
E は AD 上の点で ∠ACE = (30 - 2a)°とする。
このとき
∠EFD = 3a°であることを示せ
これが示せたら、本題は自明
題意の図は相似の意味で
一意的に定まるので
答えがもとまるよう
題意の図を作図すればよい
|
|
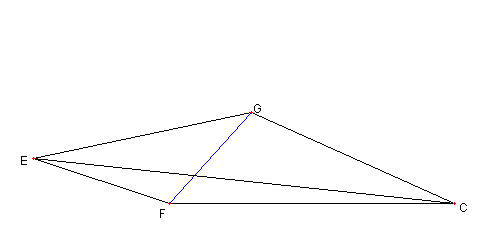
|
補題2
∠GEC = ∠GCE = (30-2a)°
∠FEC = 2a°, ∠FCE = a°
∠EGF = (30+a)°
なる四角形 EFCG を作図せよ
|
|
|
補題2を認めての補題1の図の作図
D を E から FC に下ろした垂線の足
A を DE と CG との交点とおく
これで補題1の図が得られていることを示す
|
|
|
∠DAC = 90°- ∠ACD
= (90-(30-2a)-a)°= (60+a)°
180°- ∠GFE = ∠FEG + ∠FGE
= (2a + (30-2a) + (30+a))°
= (60+a)°
であるから四辺形 AEFG は円に内接している
ここで
∠ADC = 90°
∠DAC = (60+a)°
∠DAF = ∠EGF = (30+a)°
∠ACE = (30-2a)°
であり
∠DFE = ∠FEC + ∠ECF = 3a°
となり、求める図が作図される。
|

|
補題2
∠GEC = ∠GCE = (30-2a)°
∠FEC = 2a°, ∠FCE = a°
∠EGF = (30+a)°
なる四角形 EFCG を作図せよ
これに取り組もう
|
|
正三角形 ⊿CKM を描く
MK = MG, ∠KMG = (60+2a)°の
二等辺三角形 ⊿MKG を描く
GM = GF, ∠MGF = (60+4a)°の
二等辺三角形 ⊿GFM を描く
∠GMF = (60-2a)°、∠AMK = (60+2a)°、
∠KMD = 60°
なので、 F, M, C は一直線上にある
|
|
|
∠MGC = ∠MCG = (∠GMC)/2 = (30-a)°
∠KCG = 60°- ∠MCG = (30+a)°
∠KGC = ∠KGM - ∠CGM
= (60-a)°- (30-a)°= 30°
である。
KC = KM = GM = GF である。
⊿FGE ≡ ⊿KCG なる ⊿FGE を描く
GC = GE, ∠EGF = ∠GCK = (30+a)°,
∠FEG = ∠KGC = 30°である
|
|
|
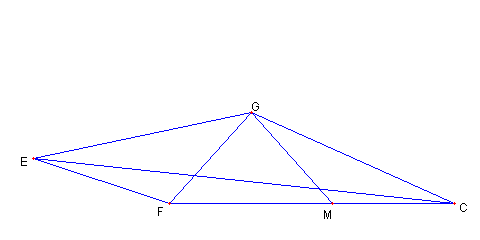
∠EGC = ∠EGF + ∠FGM + ∠MGC = ((30+a)+(60+4a)+(30-a))°
で GC = GE なので
∠GEC = ∠GCE = (30-2a)°
である。
∠FEC = ∠FED - ∠CEG = (30 - (30-2a))°= 2a°
∠ECF = ∠GCM - ∠GCE = ((30-a) - (30-2a))°= a°
であり
∠EGF = ∠GCK = (30+a)°
である。
補題2が示せた。
問題に戻る
Topに戻る
|

|
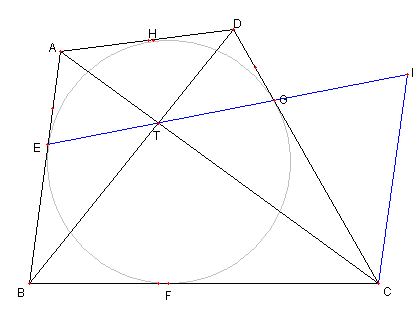
円に外接する四辺形と長さ
四辺形 ABCD は円に外接しているとする。
T を対角線 AC と BD との交点とする。
T から辺 AB, BC, CD, DA 各々に
下ろした垂線の足を各々 K, L, M, N とおく
h1 = TK,
h2 = TL,
h3 = TM,
h4 = TN
とおくとき、次が成り立つことを示せ。
1/ h1 + 1/h3 =
1/ h2 + 1/h4
|
|
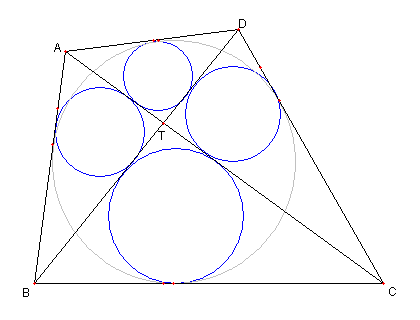
|
類題
⊿TAB, ⊿TBC, ⊿TCD, ⊿TDA 各々の内接円の
半径を
r1,
r2,
r3,
r4
とおくとき、次が成り立つことを示せ。
1/ r1 + 1/r3 =
1/ r2 + 1/r4
|
|
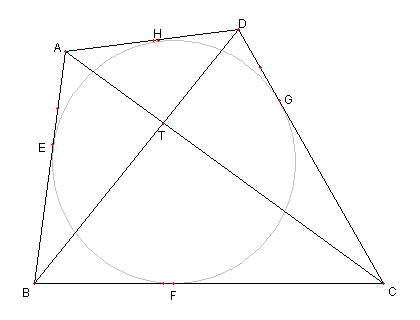
|
補題1
四辺形 ABCD の内接円と
辺 AB, BC, CD, DA との接点を各々
E, F, G, H とおく
a = AE ( = AH), b = BF ( = BF)
c = CG ( = CF), d = DH ( = DG) とおき
⊿TAB, ⊿TBC, ⊿TCD, ⊿TDA 各々の面積を
S1,
S2,
S3,
S4
とおくとき、次が成り立つことを示せ。
S1 :
S2 :
S3 :
S4 =
ab : bc : cd : da
|
|

|
補題2
補題1の記号のもと
α = TA, β = TB, γ = TC, δ TD とおくとき
次が成り立つことを示せ
① S1 :
S2 :
S3 :
S4 =
αβ : βγ : γδ : δα
② α : γ = a : c,
β : δ : b : d
|
|
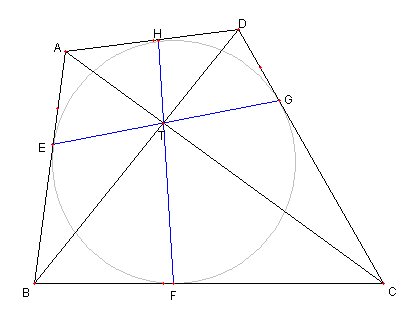
|
補題3
補題1の記号のもと
EG, HF, AC, BD は一点で交わる
ことを示せ
|

|
補題1を認めての本題の証明
2S1 = AB×h1 = (a+b)h1,
2S2 = BC×h2 = (b+c)h2,
2S3 = CD×h3 = (c+d)h3,
2S4 = DA×h4 = (d+a)h4
なので、補題1より
(a+b)h1 : (b+c)h2 : (c+d)h3 :
(d+a)h4
= ab : bc : cd : da
よって
(a+b)h1/(ab) = (b+c)h2/(bc)
= (c+d)h3/(cd) = (d+a)h4/(da)
これを t とおくと
t/h1 = 1/a + 1/b, t/h3 = 1/c + 1/d
t/h2 = 1/b + 1/c, t/h4 = 1/d + 1/a
を得て、求める結果
1/ h1 + 1/h3 =
1/ h2 + 1/h4
を得る。
|

|
補題1、2を認めての類題の証明
2S1 = (a+b+α+β)r1,
2S2 = (b+c+β+γ)r2,
2S3 = (c+d+γ+δ)r3,
2S4 = (d+a+δ+α)r4
である。補題2の ① より
(a+b+α+β)r1/(αβ)
= (b+c+β+γ)r2/(βγ)
= (c+d+γ+δ)r3/(γδ)
= (d+a+δ+α)r4/(δα)
である。これを u とおくと
u/r1 + u/r2
= (a+b)/(αβ) + (c+d)/(γδ)
+ 1/α + 1/β + 1/γ + 1/δ
u/r2 + u/r4
= (b+c)/(βγ) + (d+a)/(δα)
+ 1/α + 1/β + 1/γ + 1/δ
である。
補題2の ② より
α/a = γ/c これを v とおく
β/b = δ/d これを w とおく。このとき
αβ = vwab, γδ = vwcd,
βγ = vwbc, δα = vwda なので
(a+b)/(αβ) + (c+d)/(γδ)
= (b+c)/(βγ) + (d+a)/(δα)
よって
1/ r1 + 1/r3 =
1/ r2 + 1/r4 が示せた
|

|
補題2を認めての補題1の証明
補題2の ② より
α/a = γ/c これを v とおく
β/b = δ/d これを w とおく。このとき
αβ = vwab, γδ = vwcd,
βγ = vwbc, δα = vwda なので
αβ : βγ : γδ : δα
= ab : bc: cd : da である。
これと補題2 ① より
S1 :
S2 :
S3 :
S4 =
ab : bc : cd : da を得る
|
|
補題3を認めての補題2の証明
θ = ∠ATB とおくと
sin θ = sin (180°- θ) であり
2S1 = αβ sin θ ,
2S2 = βγsin (180°- θ),
2S3 = γδsin θ ,
2S4 = δαsin (180°- θ)
なので ① が示せた。
AB と CD が平行のときは
⊿TAB ∽ ⊿TCG なので
TA : TC = AE : CG
つまり α : γ = a : c
BA の延長と CD の延長が交わるとき
∠AET = ∠DGT である。
C を通り AB と平行な直線と
EG の延長との交点を I とおくと
⊿TAB ∽ ⊿TCI なので
TA : TC = AE : CI
また
∠CIG = ∠AET = ∠DGT = ∠CGI
よって CI = CG
TA : TC = AE : CG
つまり α : γ = a : c を得る
AB の延長と DC の延長が交わるときも
同様に α : γ = a : c を得る
故にいつも α : γ = a : c を得る
同様に β ; δ = b : d である
|

|
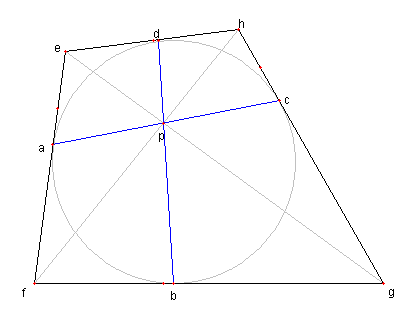
補題3の証明
単なる好みの問題ですが、
記号が変えてあります
四辺形 EFGH が円に外接し、
各辺との接点を A, B, C, D とする
AC と BC との交点を P とし
P が EG, FH 上にあることを示す。
適当に座標をいれて、四辺形の内接円を
単位円とする。
点 A ~ H、P に対応する複素数を
各々 a ~ h, p とおく
一般に a, b が長さ1の複素数とすると
a, b を通る直線の方程式きは
z + abz = ab
a での単位円の接線の方程式は
z + a2z = 2a
である。 これを使おう
|
|
p が a と c を結ぶ直線上にあり、
b と d と c を結ぶ直線上にあるので
① p + acp = a+c
p + bdp = b+d
f が単位円の a における接線上にあり
b における接線上にあるので
② f + a2f = 2a
f + b2f = 2b
h が単位円の c における接線上にあり
d における接線上にあるので
③ h + c2h = 2c
h + d2h = 2d
である。
φ = fh
+ hp
+ pf
- fh
+ hp
+ pf
とおく。
φ = 0 を示そう。これが示せたら
f, p, h が一直線上にあることがわかる。
|
① より
acp = a+c-p
bdp = b+d-p
②、③より
(a+b)f = 2
(a+b)f = 2ab
(c+d)h = 2
(c+d)h = 2ab
である。従って
|
(a+b)(c+d)φ
= (a+b)f(c+d)h
+ (a+b)(c+d)hp
+ (c+d)p(a+b)f
- (a+b)f(c+d)h
- (a+b)(c+d)hp
- (c+d)p(a+b)f
= 4ab + 2cd(a+b)p
+ 2(c+d)p
- 4cd - 2(a+b)p - 2ab(c+d)p
= 4ab - 4cd + 2cp + 2dp - 2ap - 2bp
+ 2dacp
+ 2cbdp
- 2bacp
- 2abdp
= 4ab - 4cd + 2cp + 2dp - 2ap - 2bp
+ 2d(a+c-p)
+ 2c(b+d-p)
- 2b(a+c-p)
- 2a(b+d-p) = 0
(a+b)(c+d) ≠ 0 より φ = 0 をえる
p は f と h を結ぶ直線上にある。
同様に
p は e と g を結ぶ直線上にある。
問題に戻る
Topに戻る
|

|
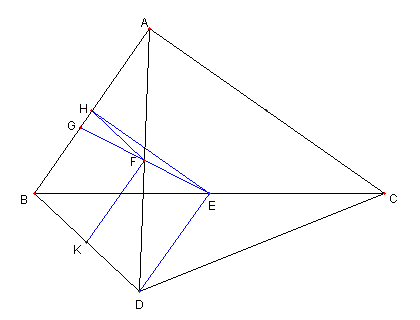
直角三角形と二等辺三角形と中点
⊿ABC は ∠BAC = 90°の直角三角形
⊿ADC は DA = DC の二等辺三角形
E は BC の中点とし、
F は AD の中点とする
このとき、次を示せ。
BD = 2EF である
|
|
|
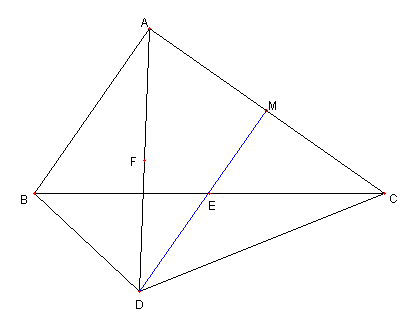
補題
今までの記号のもと
EF の延長と AB との交点を G
AB の中点を H, BD の中点を K とおく
このとき次が成り立つことを示せ
① DE と AB は平行である
② FE = FG = FH である。
③ HBKF は平行四辺形をなす。
|
|
|
① の証明
M を AC の中点とおくと
DA = DC なので
DM は AC の垂直二等分線である
BA, DM は共に AC と直交しているので
BA, DM は平行である
M が AC の中点なので、
DM は BC の中点 E を通る。
よって、 DE は BA と平行である。
|
|
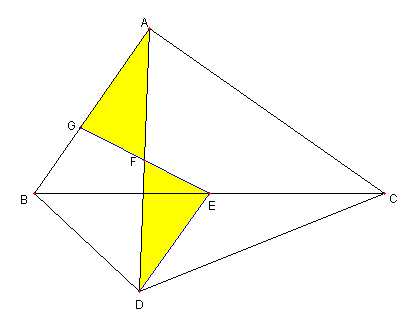
|
② の証明
DE と AG が平行で
AF = DF なので
⊿DEF ≡ ⊿AGF である
よって EF = FG
|
|
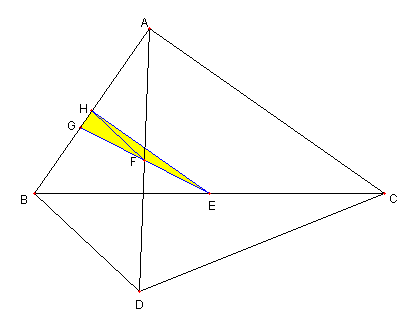
|
∠EHG = 90°で EF = FG なので
FH = FE = FG である。
② が示せた。
|
|
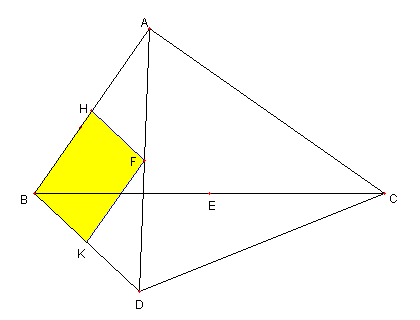
|
③ の証明
F, H, K は各々
AD, AB, BD の中点なので
HBKE は平行四辺形をなす。
問題に戻る
Topに戻る
|
|

|
円に外接する四辺形と直交する弦
四辺形 EFGH は円に外接しているとする。
その円と、辺 HE, EF, FG, GH 各々との接点を
A, B, C, D とする
4直線 EG, FH, AC, BD が一点で交わっている
(参照)
その交点を P とする。
AC と BD が直交しているとき
次が成り立つことを示せ。
PB は ∠EPF の二等分線である
四辺形 EFGH の内接円が単位円となるよう
座標をいれて、複素数平面で証明する。
単位円の幾何学
a, b を長さが 1 の複素数とするとき
a = 1/a
a, b を通る直線の方程式は
z + abz = a+b
a における単位円の接線の方程式は
z + a2z = 2a
これを使う
|
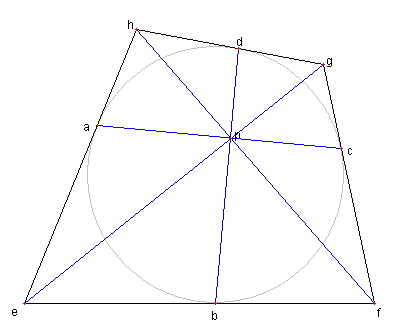
|
A ~ H に対応する複素数を a ~ h とおく
a, b, c, d は長さが 1 の複素数である。
AC と BD が直交しているので
① ac + bd = 0
である。
E が単位円の A における接線上にあるので
e + a2e
= 2a
であり、同様に
|