問題2コメント
数学的帰納法とは何かを理解していないとこの問題に有効な解答が与えられない。
「
が 13 で割り切れる」という命題を P(n) とおいたとき
P(1), P(2), ... , P(n), ....
という無限個の命題が正しいことを示せという問題である。
B さんの意見は人間は無限個のことを確かめることはできないという意見であった。
A さんの意見は始めのいくつかは確かめられるという意見であった。
有限個の操作で無限個の命題が真であることを示すのが数学的帰納法である。
(*1) P(1) が真である。
(*2) P(1),P(2),...,P(k) が真であると仮定すると P(k+1) も真である。
これを示して
P(1), P(2), ... , P(n), ....
がすべて真であることを主張しているのが数学的帰納法である。
数学的帰納法は本質的に背理法である。
(*1), (*2) が成り立ったとする。いま
P(1), P(2), ... , P(n), ....
のうちに真でないものがあったと仮定する。このとき最初に真でないものがあるはず
である。それを P(m) とする。
(*1) が成り立つので m は 1 ではない。
よって m > 1 である。m のとり方より
P(1),P(2), ... , P(m-1) が真なので (*2) より P(m) は真になる。
これは矛盾である。よって
P(1), P(2), ... , P(n), ....
はすべて真になる。
(*2) の代わりに次の (**2) を使うことが多い。((*2)を使うのが正統である。)
(**2) P(k) が真であると仮定すると P(k+1) も真である。
を f(n) とおくと
f(1)=9+4=13,
16f(k)-f(k+1) =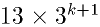 
戻る
メニューに戻る