解答
(1) (x2-ny2)(z2-nt2)
= (x-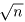 y)(x+
y)(x+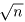 y)
(z-
y)
(z-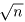 t)(z+
t)(z+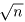 t)
= (x-
t)
= (x-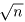 y)(z-
y)(z-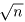 t)
(x+
t)
(x+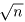 y)(z+
y)(z+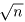 t)
t)
= ((xz+nyt)-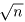 (xt+yz))((xz+nyt)+
(xt+yz))((xz+nyt)+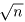 (xt+yz))
= ((xz+nyt)2-n(xt+yz)2) である。
(xt+yz))
= ((xz+nyt)2-n(xt+yz)2) である。
(2) 12-2×12 = -1 であり
32-2×22 = 1 である。
x1 = 1、y1 = 1 とおき
xn+1 = 3xn + 4yn,
yn+1 = 2xn + 3yn (n = 1,2,3,...,) とおくと
(x1,y1),
(x2,y2),
(x3,y3), ... ,
(xn,yn), ... は全て x2-2y2 = -1 の自然数解
でありあい異なる。
(x1,y1) = (1,1)
(x2,y2) = (7,5)
(x3,y3) = (41,29)
(x4,y4) = (239,169)
なので求める解の一つは (239,169) である。
戻る
メニューに戻る
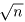 y)(x+
y)(x+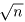 y)
(z-
y)
(z-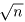 t)(z+
t)(z+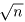 t)
= (x-
t)
= (x-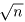 y)(z-
y)(z-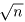 t)
(x+
t)
(x+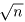 y)(z+
y)(z+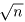 t)
t)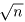 (xt+yz))((xz+nyt)+
(xt+yz))((xz+nyt)+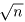 (xt+yz))
= ((xz+nyt)2-n(xt+yz)2) である。
(xt+yz))
= ((xz+nyt)2-n(xt+yz)2) である。