解答
放物線 C 上に異なる 2 点 P, Q をとり P における C の接線と Q における C の接線の交点を R とする。
いま RP = RQ とする。このとき C の軸が PQ の垂直二等分線であることを、先ず
示す。
軸を y 軸, 頂点を原点となるように、座標をいれると C の方程式は
y = mx2 の形をしている(m ≠ 0)。P, Q の x 座標を各々 p, q とすると
P(p, mp2), Q(q, mqx2) である( p ≠ q)。
RP の方程式は y = 2mpx - mp2
RQ の方程式は y = 2mqx - mq2
なので R の座標は ((p+q)/2, mpq) となる
RP = RQ より (mp2 - mpq)2 = (mq2 - mpq)2
を得るが
m ≠ 0, p - q ≠ 0 より p2 = q2 を得て、
再び p - q ≠ 0 より p + q = 0 即ち q = -p を得る。
これは C の軸が PQ の垂直二等分線であることを意味している。
さて、もとの問題に戻ろう。i を 1 ≤ i ≤ n なる自然数とする。
OPi-1 と OPi とが放物線 Ci の接線で
OPi-1 = OPi なので Ci の軸は
Pi-1Pi の垂直二等分線であり当然 O を通っている。
長さを変えないで O が原点で Ci の軸が y 軸となるように座標を取り直せば
題意より
Pi-1(-α, β),
Pi(α, β) となる。
ただし θ = π/n; とおいて α = cos θ, β =sin θ としている。
また Ci の方程式は y = ax2 + b の形で表される。
OPi は Ci の (α, β) における接線なので、
その方程式は y = 2aα(x - α) + β である。これが原点を通るので
β = 2aα2 である。
(α, β) が Ci 上にあるので β = aα2 + b。つまり
b = aα2 である。
ax2 + b - 2aα を 0 から α まで定積分すると
aα3/3 を得る。
つまり OPi-1, OPi と Ci で囲まれる図形の面積
= 2aα3/3 = αβ/3 =
(cos θsin θ)/3 = (sin 2θ)/6 = (sin 2π/n)/6 を得る。
残りの部分も同じなので Sn = n sin(2π/n)/6 となる。
Sn = n sin(2π/n)/6 = (π/3)×(sin(2π/n)/(2π/n)) なので
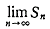 = π/3 を得る。
= π/3 を得る。
二つ戻る
戻る
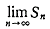 = π/3 を得る。
= π/3 を得る。