n を 3 以上の自然数とする。点 O を中心とする半径 1 の円において、
円周を n 等分する点を P0,P1,...,Pn-1 を時計回りにとる。
各 i = 1, 2, ..., n に対して、直線 OPi-1 と OPi と
それぞれ 点 Pi-1, Pi で接するような放物線を Ci とする。
ただし、Pn = P0 とする。
放物線 C1,C2,...,Cn によって囲まれる部分の面積を Sn とするとき
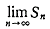を求めよ。
増加を押すと分点が増えます
問題１ 問題２ 問題５ 参照
ヒント 戻る