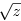解答
(1)
 +
+ 


が x = 0, y = 1 でも成り立つので 4  a が成り立つ。
a が成り立つ。
いま a = 4 とする。 y  0 として固定する。
0 として固定する。
f(x) =  +
+  -
-  とおく。
このとき
とおく。
このとき
x > 0 のとき
f'(x) = 1/(2 ) - 1/(2
) - 1/(2 )
)  0
であり f'(0) = 0 であるので
0
であり f'(0) = 0 であるので
f(x)  0 成り立つ。
0 成り立つ。
答えは a = 4 である。
(2) a = 4 とする。
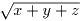 +
+ 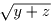 +
+ 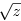


が x = 0, y = 0, z = 1 でも成り立つので 9  b が成り立つ。
b が成り立つ。
さらに b = 9 とする。 y  0、z
0、z  0
として固定する。
0
として固定する。
g(x) = 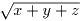 +
+ 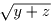 +
+ 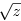 -
-  とおく。このとき
とおく。このとき
x > 0 のとき
g'(x) = 1/(2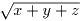 ) - 1/(2
) - 1/(2 )
)
 0 であるので
0 であるので
g(x)  g(0) = 2
g(0) = 2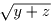 +
+ 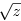 -
- 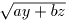 が成り立つ。
が成り立つ。
今度は z  0
として固定して y を動かす。
0
として固定して y を動かす。
h(y) = 2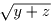 +
+ 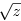 -
- 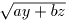 とおく。このとき
とおく。このとき
y > 0 のとき
h'(x) = 1/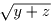 - 2/
- 2/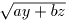
 0
が成り立つ。
0
が成り立つ。
(ay+bz = 4x+9y  4(x+y) なので上の不等式が成り立つ。)
4(x+y) なので上の不等式が成り立つ。)
よって h(y)  h(0) = 0 であるので
h(0) = 0 であるので
x  0, y
0, y  0、z
0、z  0、 のとき、
0、 のとき、
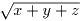 +
+ 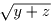 +
+ 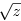


が成り立つ。よって b 最大値は 9 である。
戻る
メニューに戻る
 +
+ 


 a が成り立つ。
a が成り立つ。 0 として固定する。
0 として固定する。 +
+  -
-  とおく。
このとき
とおく。
このとき ) - 1/(2
) - 1/(2 )
)  0
であり f'(0) = 0 であるので
0
であり f'(0) = 0 であるので 0 成り立つ。
0 成り立つ。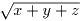 +
+ 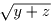 +
+ 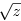


 b が成り立つ。
b が成り立つ。 0、z
0、z  0
として固定する。
0
として固定する。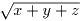 +
+ 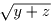 +
+ 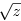 -
-  とおく。このとき
とおく。このとき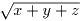 ) - 1/(2
) - 1/(2 )
)
 0 であるので
0 であるので g(0) = 2
g(0) = 2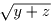 +
+ 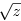 -
- 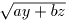 が成り立つ。
が成り立つ。 0
として固定して y を動かす。
0
として固定して y を動かす。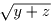 +
+ 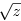 -
- 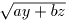 とおく。このとき
とおく。このとき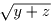 - 2/
- 2/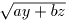
 0
が成り立つ。
0
が成り立つ。 4(x+y) なので上の不等式が成り立つ。)
4(x+y) なので上の不等式が成り立つ。) h(0) = 0 であるので
h(0) = 0 であるので 0, y
0, y  0、z
0、z  0、 のとき、
0、 のとき、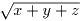 +
+ 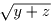 +
+