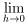(f(a+2h)-f(a-h))/h 　= 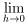3(f((a-h)+3h)-f(a-h))/(3h) これは単なる式変形なので正しい。 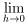3(f((a-h)+3h)-f(a-h))/(3h) = 3f'(a) の部分は等号はもちろん成立するのだが その論拠が必要である。 一般に次の命題は正しいか？ f(x) は a を含む開区間で微分可能で g(x) は 0 を含む開区間で連続で g(0) = a とする。 このとき 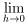(f(g(h)+h)-f(g(h)))/h = f'(a) である。 　 次に続く　　 戻る