f(x) は a を含む開区間で微分可能で
g(x) は 0 を含む開区間で連続で g(0) = a とする。
このとき
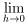(f(g(h)+h)-f(g(h)))/h = f'(a)である。
f'(x) が x = a で連続ならば、上の主張は正しい。
f'(x) が x = a で連続とする。
平均値の定理より
(f(g(h)+h)-f(g(h)))/h = f'(θ(h)) を満たすような
θ(h) が g(h)+h と g(h) の間に存在する。
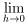θ(h) = 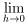g(h) = a でありf'(x) が x = a で連続なので
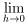f'(θ(h)) = f'(a) となる。次に続く 一つ 戻る