1m+2m+...+nmの話

1 + 2 + ... + n = n(n+1)/2
12 + 22 + ... + n2 = n(n+1)(2n+1)/6
13 + 23 + ... + n3 = n2(n+1)2/4
は良く知られた公式(証明)である。

f1(x) = x(x+1)/2, f2(x) = x(x+1)(2x+1)/6, f3(x) = x2(x+1)2/4 とおく。このとき全ての自然数 n に対して
1 + 2 + ... + n = f1(n)
12 + 22 + ... + n2 = f2(n)
13 + 23 + ... + n3 = f3(n)
が成り立っている。
一般に次の定理が成り立つ(略証明)。

定理１　m を自然数とするとき m+1 次の多項式 fm(x) で 全ての自然数 n に対して
1m + 2m + ... + nm = fm(n)
を満たすものが唯一つ存在する。

多項式 fm(x) に対しては次の定理が成り立つ (略証明)。

定理２
(1)　m を 2 以上の偶数とするとき fm(x) は x(x+1)(2x+1) で割り切れる。
(2)　m を 3 以上の奇数とするとき fm(x) は x2(x+1)2 で割り切れる。

定理２の証明において重要な役目を果たしたのが次の補題である。

補題１　m を自然数とするとき次が成り立つ。
(1)　fm(x+1) = fm(x) + (x+1)m
(2)　fm(1) = 1, fm(0) = 0, fm(-1) = 0
(3)　(-1)m+1fm(x) = fm(-(x+1))

補題１の(1),(2) は次の定理３を証明するのにも重要な役割をはたす (略証明)。

定理３　m を自然数とするとき 。
　　
ここで a は fm+1(1) = 1 をみたす実数であるが m が 2 以上の偶数のときは a = 0 である。

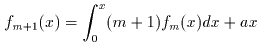
f1(x) = x2/2 + x/2
f2(x) = x3/3 + x2/2 + x/6
f3(x) = x4/4 + x3/2 + x2/4
f4(x) = x5/5 + x4/2 + x3/3 - x/30
f5(x) = x6/6 + x5/2 + 5x4/12 - x2/12
f6(x) = x7/7 + x6/2 + x5/2 - x3/6 + x/42
f7(x) = x8/8 + x7/2 + 7x6/12 - 7x4/24 + x2/12
f8(x) = x9/9 + x8/2 + 2x7/3 - 7x5/15 + 2x3/9 - x/30
 　 f1(x) = x(x+1)/2
f2(x) = x(x+1)(2x+1)/6
f3(x) = x2(x+1)2/4
f4(x) = x(x+1)(2x+1)(3x2+3x-1)/30
f5(x) = x2(x+1)2(2x2+2x-1)/12
f6(x) = x(x+1)(2x+1)(3x4+6x3-3x+1)/42
f7(x) = x2(x+1)2 (3x4+6x3-x2-4x+2)/24
f8(x) = x(x+1)(2x+1)(5x6 + 15x5 + 5x4 - 15x3 - x2 + 9x - 3)/90


f2(x),f3(x),f4(x),f5(x), f6(x),f7(x) の x の係数は
1/6, 0, -1/30, 0, 1/42, 0, -1/30 である。
これはベルヌイ数 B2,B3,B4,B5, B6,B7,B8 に一致している。

問題
　n ≥ 2 のとき fn(x) の x の係数は ベルヌイ数 Bn に一致する。
上の命題は正しいか？

ここでベルヌイ数の定義を与えておく。

ベルヌイ数の定義
ベルヌイ数 Bn は次の式で定義される。
x/(ex-1) = B0 + B1x + (B2/2)x2 + (B3/3!)x3 + (B4/4!)x4 + (B5/5!)x5 + (B6/6!)x6 + (B7/7!)x7 + (B8/8!)x8 + (B9/9!)x9 + ...








正しいことが知られている。
(問題の解答)。



戻る