|
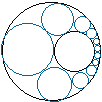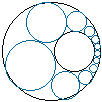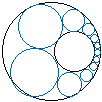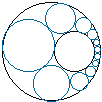
1 次の問いに答えなさい (1) 直線 y = 2x + 9 が、円 x2 + y2 + 2x - 4y = 4 によって切り取られる線分の長さを求めなさい。 (2) xe-x を 0 から 1 まで定積分した値を求めよ。 (3)
2 四面体 OABC において、v(OA) = v(a), v(OB) = v(b), v(OC) = v(c) とするとき、 次の問いに答えなさい。 (1) 点 P が 3 点 A, B, C で定まる平面上にあるとき、実数 r, s, t を用いて v(OP) = r v(a) + s v(b) + t v(c) (r + s + t = 1) と表されることを示しなさい。 (v(OP) は O を始点 P を終点とするベクトルを表すことにする。) (2) 辺 OA を 3 : 5 に内分する点を K, 辺 BC を 5 : 3 に内分する点を L とし、 線分 KL の中点を M とするとき イ v(OM) を v(a), v(b), v(c) で表しなさい。 ロ 直線 OM と ⊿ABC の交点を P とするとき v(OP) を v(a), v(b), v(c) で表し OM : MP の比を求めなさい。 3 関数 y = cos2θ + root(3) sin θ cos θ - a sin θ - root(3) a cos θ がある。 t = sin θ + root(3) cos θ とするとき、次の問いに答えなさい。 ただし a は実数の定数とする。 (1) t のとりうる値の範囲を求めなさい。 (2) 関数 y を t で表しなさい。 (3) 関数 y の最大値、最小値を求めなさい。ただし、そのときの θ の値を 求めなくてもよい。 4 別載 5 次の問いに答えなさい。 (1) 「関数 f(x) = log x (対数は自然対数)の導関数を定義に従って求める」ことを 生徒に指導するとき、 あなたが指導者として、数学的に大切であると考えるポイントを 3 つ、例に従って 述べなさい。 例 「関数 y = x2 sin x を微分する」 ポイント1 積の導関数 (uv)' = u'v + uv' ポイント2 三角関数の導関数 (sin x)' = cos x ポイント3 xn の導関数 (xn)' = n xn-1 (2) イ 曲線 y = log x に原点から引いた接線の方程式を求めなさい。 ロ 直線 y = x と曲線 y = loga x (a > 0, a ≠ 1) との共有点の個数を、定数 a の値で分類して求めなさい。 解答 1(1)(2) 1(3) 2 3 5(1) 5(2) |