ddlA で増加・減少をおすと
円の中心が変化します。
ddlB で増加・減少をおすと
円の半径が変化します。
１ 1 から n (n ≥ 2)までの番号、順番に１つずつ書かれた n 枚の 札が袋に入っている。
この袋の中から札を 1 枚ずつ取り出し、次の (i),(ii) のルールに従って A または B の箱に入れる。
(i) 最初に取り出した札は A の箱に入れる。
(ii) 2 番目以降にとしだした札は
その番号がそれまでに取り出した札の番号のどれよりも大きければ A の箱にいれ、
そうでなければ B の箱にいれる。
n 枚の札をすべて取り出し、箱に入れ終わったとき、
B の箱にちょうど１枚の札が入っている確率を求めよ。
２ 楕円 x2 + y2/4 = 1 と円 (x-a)2 + y2 = b (b >0)が相異なる 4 点で交わるという。
このときの点 (a,b) のとりうる範囲を図示せよ。
３ 各面が鋭角三角形である四面体 ABCD において 辺 AB と辺 CD は垂直でないとする。
このとき辺 AB を含む平面 α に点 C, 点 D から下ろした垂線の足を それぞれ C', D' とするとき、
4 点 A, B, C', D' がすべて相異なりしかも同一円周上にあるように とれることを示せ。
４ f(x) は xn の係数が 1 である x の n 次式である。
相異なる n 個の有理数 q1, q2, ..., qn に対して f(q1), f(q2), ..., f(qn) がすべて 有理数であれば、
f(x) の係数はすべて有理数であることを、数学的帰納法を用いて示せ。
５ 数列 {an}, {bn} を a1 = 3, b1 = 2, an+1 = an2 + 2bn2, bn+1 = 2anbn で定める。このとき
(1) an2 - 2bn2 を求めよ。
(2) n
∞ のときの an/bn の極限値を
求めよ。６ 閉区間 [-π/2,π/2] で定義された関数 f(x) が
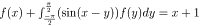(-π/2 ≤ x ≤ π/2)を満たしている。f(x) を求めよ。
| １の解答 | ２の解答 | ３の解答 | |
| ４の解答 | ５の解答 | ６の解答 |
(計算間違い等がありましたら知らせて下さい)