１ 正の数からなる数列 {an} が次の条件 (i),(ii) をみたすとき、
の初項から第 n 項 an までの和 a1 + a2 + ... + an を求めよ。
(i) a1 = 1, (ii) log an - log an-1 = log(n-1)- log(n+1) (n ≥ 2)
２ f(x) = x sin x (x ≥ 0) とする。 点 (π/2,π/2) における y = f(x) の法線と
y = f(x) のグラフの 0 ≤ 0 ≤ π/2 の部分、 および y 軸とで囲まれる図形を考える。
この図形を x 軸周りに回転して得られる回転体の体積を求めよ。
３ 四面体 OABC は次の２つの条件
(1) OA⊥BC, OB⊥CA,OC⊥AB
(2) ４つの面の面積がすべて等しい
をみたしている。このとき、この四面体は正四面体であることを示せ。
４ 多項式 (x100+1)100 + (x2+1)100 + 1 は 多項式 x2+x+1 で割り切れるか。
５ a,b,c,d を実数とする。２次の正方行列 A =
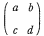と２次の単位行列 E に対して、集合 L(A) をL(A) = {rE + sA | r と s は実数}
とする。このとき次の条件(*)が成立するための a,b,c,d についての必要十分条件を求めよ。
(*) L(A) の要素 B は零行列でなければ逆行列をもつ。
６ n チームがリーグ戦を行う。すなわち、各チームは他のすべてのチームとそれぞれ 一回ずつ対戦する。引き分けはないものとし、かつ確率はすべて 1/2 で、各回の勝敗は独立に きまるものとする。このとき、(ｎ−２)勝１負のチームがちょうど２チームである確立を求めよ。 ただし、ｎ は３以上とする。
| １の解答 | ２の解答 | ３の解答 |
| ４の解答 | ５の解答 | ６の解答 |