2. (4x3 - 5x2+1)3 を x2-x+1 でわったときの余りを求めなさい。
3. 方程式 x3+ y3 + 3xy - 1 = 0, x2+ y2 = 2 をとけ
4. A =
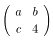で A2 = O を満たしている。A の各成分を入れ替えても逆行列が存在しないとき a, b の値を求めよ。
5. 僊BC の外接円の中心を O としたとき v(OA)+v(OB)+v(OC) = v(0) ならば 僊BC は正三角形になることを示せ。 (v(PQ) で P を始点とし Q を終点とするベクトルを表し、v(0) でゼロベクトルを表している)
6. 図において ∠ABE = ∠EBC = ∠EAC で F は AE を 2:1 に外分する点とする。
このとき ∠ACF = 90°であることを示せ。
7. AB = AC, BC = 4 の直角二等辺三角形がある。
この三角形に内接する楕円のうち面積が最大になるときのその値を求めよ。
8. y -x < 0, y+x+4 < 0, ax+by+1 < 0 が三角形をつくるとき
(a,b) がその三角形に含まれるような (a,b) の領域を図示せよ。
(多分これは記憶違いでしょう) 9. f(x) =
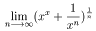とするとき y = 4 とで囲まれる
部分の面積を求めよ。10. 黒玉１０個、白玉２０個入った袋がある。１個ずつ玉を取り出し、 取り出した玉はふくろに戻さない。このときｎ回目に(はじめて？)黒玉がでる確率を Pn とする。Pn が最大になる n を求めよ。